Beschreibe die drei Geraden jeweils durch eine Gleichung von der Art y = ? · x + ?.
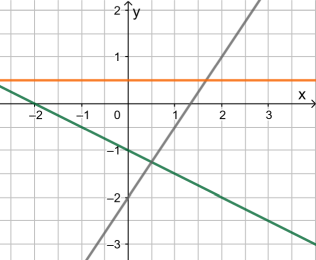
- - - - - - - - - - - Schwarz:
Für x = 0 ergibt sich y = -2, also hat der Summand am Ende des Terms den Wert -2.
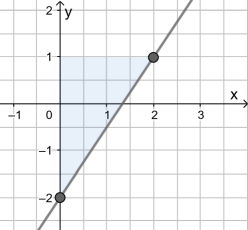
Am sogenannten Steigungsdreieck erkannt man: Nimmt x um 2 Einheiten zu, so nimmt y um 3 Einheiten zu, also hat der Faktor vor x den Wert 3/2 .
- - - - - - - - - - - Grün:
Für x = 0 ergibt sich y = -1, also hat der Summand am Ende des Terms den Wert -1.
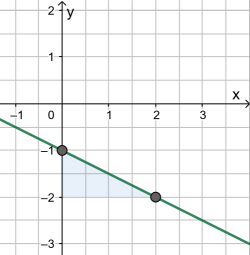
Nimmt x um 2 Einheiten zu, so nimmt y um 1 Einheit ab, also hat der Faktor vor x den Wert -1/2 ("Minus" da "abnehmend").
- - - - - - - - - - - Orange:
y ist immer 0,5 (unabhängig von x), also lautet die Gleichung y = 0,5 (das heißt der Faktor vor x hat den Wert 0).