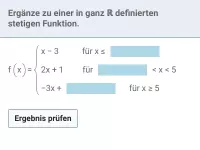
Was bedeutet es, wenn eine Funktion als stetig oder unstetig bezeichnet wird, und was ist ein Beispiel für eine unstetige Funktion?
Die Graphen mancher Funktionen weisen an bestimmten Stellen ihrer Definitionsmenge Sprünge auf. Man nennt die Funktion dann an solchen Stellen unstetig (ansonsten stetig). Ist eine Funktion an jeder definierten Stelle stetig, so nennt man sie (insgesamt) stetig.
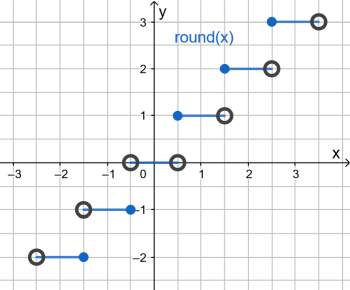
Bei den bisher behandelten Funktionstypen (ganzrational, gebrochen-rational, exponentiell, trigonometrisch) handelt es sich um stetige Funktionen. Dagegen ist z.B. die Rundungsfunktion, die jeder reellen Zahl den auf Ganze gerundeten Wert zuordnet, nicht stetig (siehe Abbildung).

Erläuterung: "Knödel" und "Kringel" verdeutlichen, ob der jew. Punkt zum Graphen G gehört oder nicht. Z.B. gilt (0,5|0) ∉ G, aber (0,5|1) ∈ G (weil bei 0,5 auf 1 aufgerundet wird).
Siehe auch