Was versteht man unter einer abschnittweise definierten Funktion und wie prüft man ihre Stetigkeit?
Funktionen können auch durch mehrere Funktionsterme definiert sein, die jeweils in bestimmten Abschnitten der Gesamtdefinitionsmenge gelten. Man spricht von abschnittsweise definierten Funktionen.
Bei solchen Funktionen können an den Nahtstellen, also dort, wo die Abschnitte aufeinandertreffen, Unstetigkeitsstellen auftreten. Um die Funktion an einer Nahtstelle auf Stetigkeit zu überprüfen, setzt man diese in die Funktionsterme der beiden angrenzenden Abschnitte ein. Ergeben sich unterschiedliche Termwerte, so liegt eine Unstetigkeitsstelle vor. Ansonsten ist die Funktion dort stetig.
Beispiel 1
Überprüfe auf Stetigkeit.
| = |
|
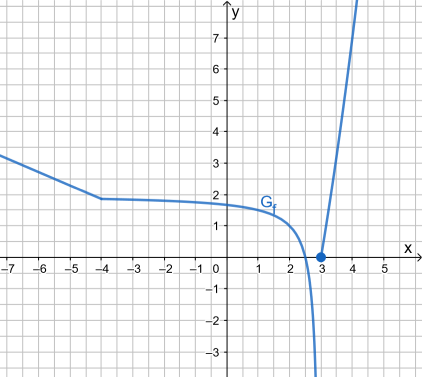
f setzt sich aus einem linearen (oben), einem gebrochen-rationalen (Mitte) und einem quadratischen (unten) Funktionsterm zusammen. Definiert ist f in ganz ℝ, da sich die angegebenen Definitionsintervalle zu ℝ vereinen. Es ist bei der Angabe einer solchen Funktion darauf zu achten, dass sich die Abschnitte nicht überlappen, sonst liegt keine Funktion vor!
Überprüfung der Stetigkeit an den Nahtstellen:
|
|
| ||||||||||||||||||
|
|
| ||||||||||||||||||
|
|
| ||||||||||||||||||
|
|
| ||||||||||||||||||
|
|
|
An der Nahtstelle
ergibt sich derselbe Termwert, also ist die Funktion dort stetig.
x | = |
|
An der Nahtstelle
kann nur für den unteren Term ein Termwert angegeben werden, der Graph macht hier einen Sprung - also ist die Funktion dort unstetig.
x | = | 3 |
Damit ist die Funktion insgesamt nicht stetig.
Bemerkung: wäre der letzte Term nur für
(ohne Gleichheitszeichen) definiert, so wäre
eine Definitionslücke und damit könnte dort überhaupt keine Steigkeitsaussage getroffen werden. In diesem Fall wäre f dann stetig (da an jeder definierten Stelle stetig).
| 3 |
x | = | 3 |
Beispiel 2
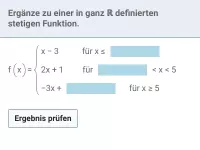
Ergänze zu einer in ganz ℝ definierten stetigen Funktion.
| = |
|
Die ersten beiden Eingabefelder fragen nach der passenden Nahtstelle. Diese muss so gewählt sein, dass die beiden "angrenzenden" Terme dort denselben Wert aufweisen. Also muss man diese gleichsetzen und nach x auflösen:
| = |
|
| |||||||||||||||||||
| = |
| x ausklammern | |||||||||||||||||||
| = |
| ||||||||||||||||||||
Bis hierhin lässt sich ohne weitere Rechnung die Lösung
angeben. Diese scheidet als Nahtstelle für die ersten beiden Terme allerdings aus, da 0 bereits Nahtstelle des mittleren und untersten Terms ist. Die erste Nahtstelle muss definitiv kleiner als 0 sein. Also knöpfen wir uns den zweiten Faktor in der Gleichung oben vor:
| = | 0 |
| = |
| Vieta | ||||||||||
| = |
| |||||||||||
| = |
| |||||||||||
Hinweis: Alternativ hätte man natürlich auch die MNF oder die p-q-Formel verwenden können, um diese beiden Lösungen zu ermitteln. "3" scheidet als Nahtstelle aus besagten Gründen ebenfalls aus, also bleibt als einzige Möglichkeit für die erste Nahtstelle
.
|
Das unterste Eingabefeld verlangt die Richtigstellung des entsprechenden Terms, so dass dieser an der Nahtstelle
denselben Wert wie der mittlere Term aufweist. Sei also z die gesuchte Zahl, so kann man folgende Gleichung aufstellen:
x | = | 0 |
| = |
| ||||||||||||||||
| = |
|
| |||||||||||||||
| = |
| ||||||||||||||||
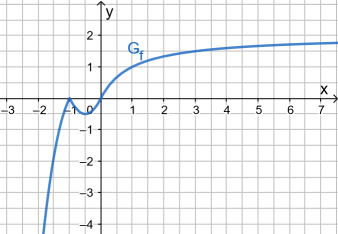
Hier zusammengefasst die stetige Funktion:
| = |
|
Siehe auch