Was sind die verschiedenen Arten von Mittelwerten und wann sind sie jeweils am besten geeignet?

Verschiedene Mittelwerte:

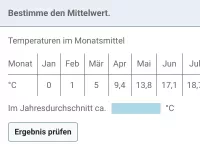
Arithmetisches Mittel:

Addiere alle Daten und dividiere die erhaltene Summe durch die Anzahl der Daten.
Dies ist der gängigste Mittelwert.
Beispiel: Notendurchschnitt berechnen.

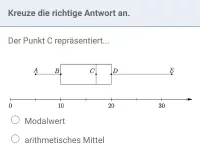
Median (Zentralwert):

Sortiere alle Daten der Größe nach und ermittle dann den Wert in der Mitte der Liste. Am einfachsten streicht man dazu gleichzeitig den ersten und letzten, dann den zweiten und vorletzten, ... Wert der Liste durch, bis der mittlere Wert übrig bleibt.
Bei einer geraden Anzahl von Daten bleiben zwei Werte in der Mitte übrig. Der Median ist in diesem Fall das arithmetische Mittel dieser beiden Zentralwerte.
Der Median wird durch einen Ausreißer-Wert nicht beeinflusst, im Gegensatz zum arithmetischen Mittel. Darum wird er z.B. für die Ermittlung des Durchschnittseinkommens verwendet. Andernfalls würden wenige Superreiche das Bild verzerren.

Modalwert:

Ermittle den Wert in der Datenmenge, der am häufigsten vorkommt.
Beispiel: Ein Schuhgeschäft sollte die am häufigsten gebrauchte Schuhgröße (Modalwert) besonders oft vorrätig haben und nicht Schuhe in der mittleren (arithmetisches Mittel) Größe aller Menschen.

Beispiel

Daten (z.B. erzielte Noten in den sechs Klassenarbeiten):
2 2 4 3 2 3

Arithmetisches Mittel:

Median:

Modalwert:

Arithmetisches Mittel

Addiere alle Daten (2+2+4+3+2+3=16) und dividiere durch die Anzahl der Daten (=6).

Arithmetisches Mittel (gerundet auf eine Stelle nach dem Komma): 2,7

Median und Modalwert

Ordne zuerst die Daten der Größe nach:

2 2 2 3 3 4

Da die Liste aus sechs Zahlen besteht, gibt es keinen Wert genau in der Mitte. Daher wird aus den beiden mittleren Werten 2 und 3 das arithmetische Mittel gebildet:

Median (Zentralwert): 2,5

Der häufigste Wert ist in der geordneten Liste einfach abzulesen:

Modalwert (häufigster Wert): 2

Siehe auch