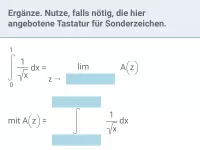
Was versteht man unter einem uneigentlichen Integral?

Sofern der Grenzwert rechts exisitiert, definiert man: \[ \int_{a}^{\infty} f(x) \, dx := \lim_{z \to \infty} \int_{a}^{z} f(x) \, dx \] und spricht von einem uneigentlichen Integral.

Analog definiert man, falls \(f(b)\) nicht definiert ist, aber der Grenzwert rechts existiert:

\[ \int_{a}^{b} f(x) \, dx := \lim_{z \to b} \int_{a}^{z} f(x) \, dx \]
Beispiel
Schreibe als Grenzwert.
(a)   
∞
0
e
−
x
 
dx
(b)   
2
1
ln
x
−
1
 
dx
Zu (a)
∞
0
e
−
x
 
dx
=
lim
z→
∞
 
A
z
mit 
A
z
=
z
0
e
−
x
 
dx

Zu (b)
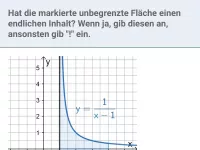
Der gegebene Ausdruck ist ein uneigentliches Integral, da der Integrand 
ln
x
−
1
 für 
x
=
1
, also für die untere Integrationsgrenze, nicht definiert ist (Argument "0" für ln). Mit "z" ist also offenbar die variable untere Integrationsgrenze gemeint, die gegen 1 strebt:
2
1
ln
x
−
1
 
dx
=
lim
z→
1
 
A
 
z
mit 
A
 
z
=
2
z
ln
x
−
1
 
dx
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.