Wie berechnet man die Oberfläche eines Kegels und beschreibt sein Netz?
Netz und Oberflächeninhalt eines Kegels
Die Oberfläche eines Kegels setzt sich zusammen aus:
- Grundfläche G: ein Kreis mit Radius r
- und Mantelfläche M: ergibt abgewickelt einen Kreissektor mit Kegelspitze als Mittelpunkt und Mantellinie s als Radius. Die Bogenlänge b des Kreissektors ist genauso lang wie der Umfang des Grundflächenkreises (b = 2 π · r).
Der Oberflächeninhalt O eines Kegels ist:
O = G + M = π · r2 + π · r · s
Beispiel 1
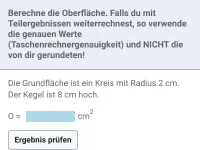
Ein 2,5 dm hoher Kegel hat eine Grundfläche, deren Durchmesser 16 cm beträgt. Berechne die Oberfläche des Kegels.
O ≈ |
|
Lösung:
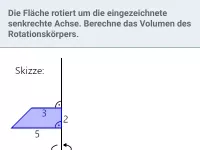
Der gegebene Kegel sieht folgendermaßen aus (nicht maßstabsgetreu):
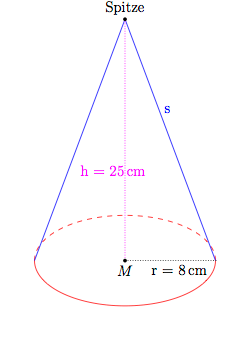
- Grundfläche
Die Grundfläche ist ein Kreis mit Radius 8 cm.
| = |
|
- Mantelfläche
In der Formel für den Mantelflächeninhalt taucht die Länge der Mantellinie s auf. Diese kann mithilfe des Satzes von Pythagoras aus dem gegebenen Radius und der Höhe berechnet werden:
| = |
|
s | = |
|
| = |
|
Damit ergibt sich für die Mantelfläche:
| = |
|
- Oberfläche des Kegels
O | = |
|
= |
|
≈ 860,77 |
|
- Erklärung und Vertiefung
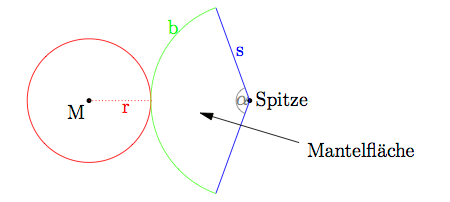
Die Mantelfläche ist abgewickelt ein Kreissektor mit Radius s und Mittelpunktswinkel α. Die Länge der Mantellinie s kann - sofern sie nicht gegeben ist - mithilfe des Satzes von Pythagoras aus Radius und Höhe berechnet werden.
Der Mittelpunktswinkel α kann über die Bogenlänge b des Kreissektors ermittelt werden. Es gilt:
b | = |
|
und
b | = |
|
Durch Gleichsetzen beider Formeln ergibt sich folgender Zusammenhang:
| = |
|
| |||||||||||||||||||||
| = |
| ||||||||||||||||||||||
Für den Flächeninhalt der Mantelfläche ergibt sich damit die Formel:
M | = |
|
M | = |
|
M | = |
|
Beispiel 2
Der Radius der Kegelgrundfläche ist 0,4 cm lang. Die Länge der Mantellinie beträgt 12 mm. Berechne die Oberfläche des Kegels.
O ≈ |
|
Lösung:
Der gegebene Kegel sieht folgendermaßen aus (nicht maßstabsgetreu):
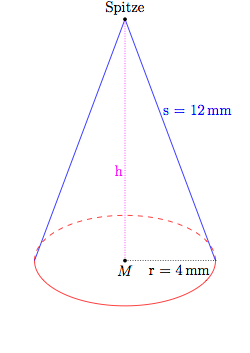
- Grundfläche
Die Grundfläche ist ein Kreis mit Radius 4 mm.
| = |
|
- Mantelfläche
| = |
|
- Oberfläche des Kegels
O | = |
|
= |
|
= |
|
- Erklärung und Vertiefung

Die Mantelfläche ist ein Kreissektor mit Radius s und Mittelpunktswinkel α. Die Länge der Mantellinie s kann - sofern sie nicht gegeben ist - mithilfe des Satzes von Pythagoras aus Radius und Höhe berechnet werden.
Der Mittelpunktswinkel α kann über die Bogenlänge b des Kreissektors ermittelt werden. Es gilt:
b | = |
|
und
b | = |
|
Durch Gleichsetzen beider Formeln ergibt sich folgender Zusammenhang:
| = |
|
| |||||||||||||||||||||
| = |
| ||||||||||||||||||||||
Für den Flächeninhalt der Mantelfläche ergibt sich damit die Formel:
M | = |
|
M | = |
|
M | = |
|
Siehe auch