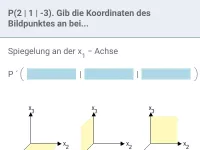
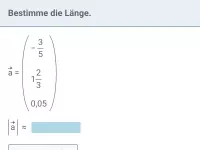
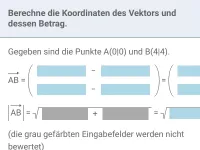
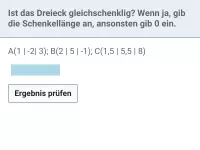
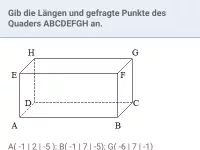
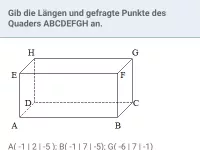
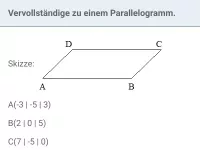
Wie berechnet man die Länge eines Vektors?
Die Länge eines Vektors erhält man, indem man seine Koordinaten quadriert, summiert und dann die Wurzel zieht. Die Vorzeichen der Koordinaten spielen dabei keine Rolle.
Beispiel 1
| = |
|
| = |
|
Beispiel 2
| = |
|
Lösung:
| = |
|
| = |
|
- - - - - - - - - - - - - - - - - - - - -
Hier eine Erklärung für die Formel im zweidimensionalen Fall:
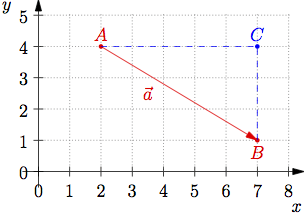
Am Bild ist zu erkennen, dass im rechtwinkligen Dreieck ABC der Satz des Pythagoras angewendet werden kann. Es gilt:
| = |
|
Auch im dreidimensionalen Fall läuft es auf Pythagoras hinaus:
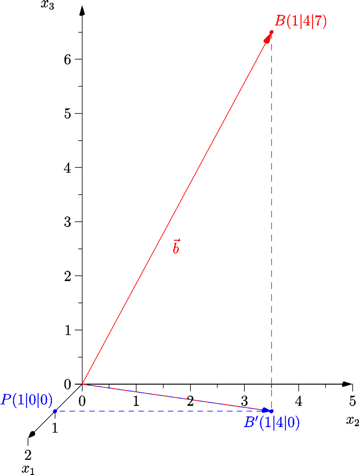
Der Ortsvektor zum Punkt B(1|4|7) entspricht dem Vektor |
|
Der Punkt B' ist die Projektion von B in die x1x2-Ebene. Das Hilfsdreieck 0PB' ist eben und rechtwinklig im Punkt P. Hier können wir Pythagoras anwenden:
| = |
|
Das Dreieck 0B'B ist ebenfalls eben und rechtwinklig in B'. Hier können wir also erneut Pythagoras anwenden und das Zwischenergebnis von eben verwenden:
| = |
| ||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||
Siehe auch