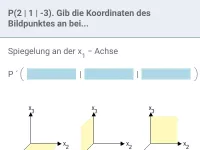
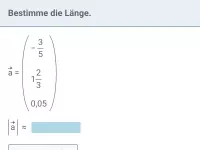
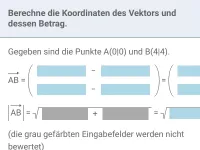
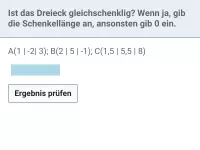
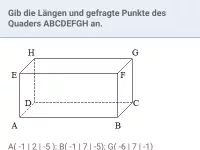
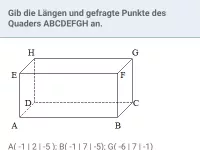
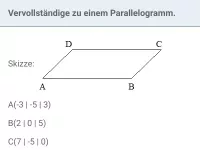
Wie berechnet man die Koordinaten eines Vektors von Punkt A nach Punkt B?
Die Koordinaten des Vektors mit Fuß in A und Spitze in B erhält man durch die Rechnung "Spitze − Fuß", also
b1 − a1
b2 − a2
b3 − a3
Beispiel
Bestimme die Verbindungsvektoren von A(7|1) nach B(2|4) und von P(1|2|3) nach Q(3|-1|4)
| ; |
|
Lösug: Spitze minus Fuß, also
| = |
|
| = |
|
- - - - - - - - - - - - - - - - - -
Falls dich interessiert, warum man so rechnet, kannst du hier weiterlesen:
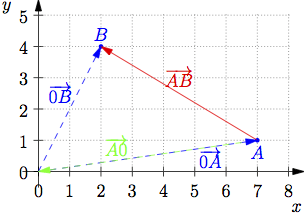
Der Verbindungsvektor von A nach B ist die direkte Verbindung von A nach B. Um diesen zu berechnen, kannst du genauso gut den "Umweg" von A über den Ursprung nach B "laufen":
| = |
| ||||||||
|
| = |
| ||||||||
|
| = |
| ||||||||
|
| = |
| ||||||||
Im dreidimensionalen Raum fällt die Vorstellung meist etwas schwerer, aber anhand des Bildes ist zu erkennen, dass genauso wie im zweidimensionalen gilt: "Spitze − Fuß":
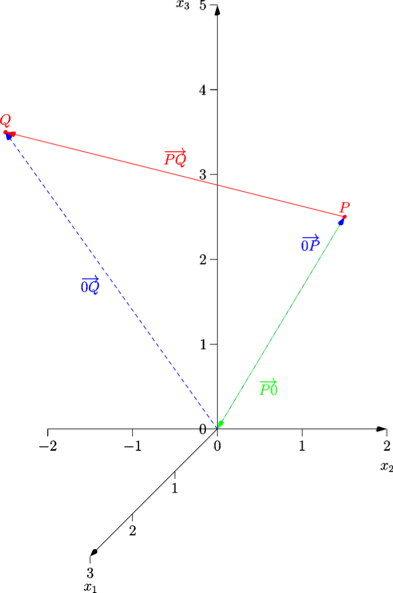
Siehe auch