Was bedeuten und wie berechnet man das arithmetische Mittel und die Standardabweichung einer Datenreihe?

Mittelwert und Standardabweichung einer Datenreihe x1, x2, ..., xn:

Mittelwert (Arithmetisches Mittel) x:

  • Addiere alle Daten und dividiere durch die Anzahl der Daten.
  • x=1/n · (x1 + x2 + ... + xn)

Empirische Standardabweichung s:

Die Standardabweichung ist ein Maß dafür, wie sehr die Werte der Datenreihe um den Mittelwert schwanken.

Berechnung der Standardabweichung:

  • Bestimme den Mittelwert x.
  • Subtrahiere den Mittelwert von jedem Wert xi der Datenreihe.
  • Quadriere jeweils die Ergebnisse.
  • Addiere alle quadrierten Werte.
  • Dividiere dann durch die Anzahl n der Daten.
  • Ziehe vom Ergebnis die Quadratwurzel.
  • Als Formel: s = √{ 1/n·[ (x1 − x)2+ (x2 − x)2 + ... + (xn − x)2 ] }

Beispiel
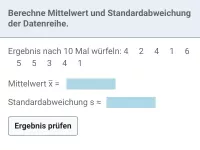
Am Schuljahresende blickt Anton auf seine Ergebnisse der 6 Mathearbeiten zurück: 2     2     4     2     1     3
Berechne Mittelwert und Standardabweichung
  • Mittelwert
x
=
2
+
2
+
4
+
2
+
1
+
3
6
=
14
6
=
7
3
=
2,
3
 
≈
 
2,3
  • Standardabweichung
s
=
2
−
7
3
2
+
2
−
7
3
2
+
4
−
7
3
2
+
2
−
7
3
2
+
1
−
7
3
2
+
3
−
7
3
2
6
=
−
1
3
2
+
−
1
3
2
+
5
3
2
+
−
1
3
2
+
−
4
3
2
+
2
3
2
6
=
1
9
+
1
9
+
25
9
+
1
9
+
16
9
+
4
9
6
=
48
9
6
=
16
3
6
=
8
9
=
2
3
2
 
≈
 
0,9
Alternative Lösung, um die lange Wurzel zu vermeiden:
Note
Abweichung vom Mittelwert
Quadrat der Abweichung
2
−
1
3
1
9
2
−
1
3
1
9
4
5
3
25
9
2
−
1
3
1
9
1
−
4
3
16
9
3
2
3
4
9
s
=
3
·
1
9
+
25
9
+
16
9
+
4
9
6
=
48
9
6
=
2
3
2
 
≈
 
0,9
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen