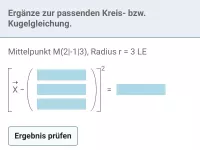
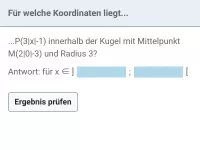
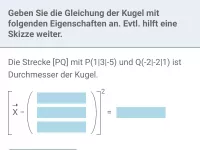
Welche Eigenschaft haben alle Punkte X auf einer Kugel mit Mittelpunkt M und Radius r, beschrieben durch Vektoren?

Alle Punkte X auf der Kugel mit Mitelpunkt M und Radius r haben die Eigenschaft, dass der Verbindungsvektor von M zu X die Länge r hat. Entsprechend lässt sich die Kugelgleichung formulieren.
Beispiel
Gib eine Gleichung der Kugel mit Mittelpunkt M(1|0|-2) und Radius 5 an.
Idee: Für jeden Punkt X der Kugeloberfläche gilt 
MX
=
5
. Aus diesem Ansatz ergeben sich alle üblichen Darstellungsformen der Kugel:
MX
=
5
X
−
M
=
5
X
−
1
0
−
2
2
=
25
    
    
Vektordarstellung
x
1
−
1
x
2
−
0
x
3
−
−
2
2
=
25
x
1
−
1
x
2
x
3
+
2
2
=
25
x
1
−
1
2
+
x
2
2
+
x
3
+
2
2
=
25
    
    
Koordinatendarstellung
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen