Wie konstruiert man geometrische Objekte wie Lotgeraden, Lotebenen und führt Spiegelungen durch?
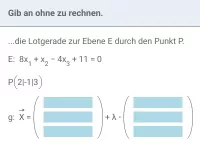
Für die Lotgerade g zu einer Ebene E durch einen Punkt P wählt man:
Spiegelungen von geometrischen Objekten an anderen führt man durch wie folgt:
- P als Aufhängepunkt und
- den Normalenvektor von E als Richtungsvektor.
- P als Aufhängepunkt und
- den Richtungsvektor von g als Normalenvektor.
Spiegelungen von geometrischen Objekten an anderen führt man durch wie folgt:
- Spiegelung eines Punkts P an einer Geraden g: Bestimme die Lotebene E zu g durch P. Der Schnittpunkt S von E und g ist der Lotfußpunkt. Schließlich addiert man zum Ortsvektor von S den Verbindungsvektor von P und S.
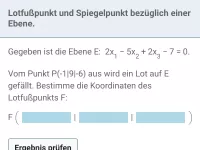
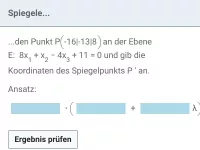
- Spiegelung eines Punkts P an einer Ebene E: Bestimme die Lotgerade g zu E durch P. Der Schnittpunkt S von E und g ist der Lotfußpunkt. Schließlich addiert man zum Ortsvektor von S den Verbindungsvektor von P und S.
- Spiegelung einer Geraden g an einer Ebene E: Spiegle zwei Punkte von g an der Ebene E und stelle die Gerade durch die gespiegelten Punkte auf.