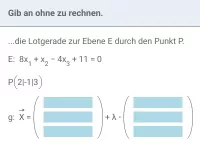
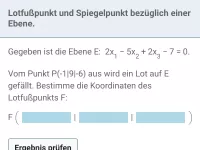
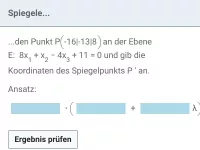
Wie bestimmt man die Lage einer Geraden zu einer Ebene und findet einen Schnittpunkt?
Eine Gerade g und eine Ebene E sind genau dann parallel, wenn der gegebene Richtungsvektor von g und der gegebene Normalenvektor von E senkrecht zueinander sind.
Abgesehen davon kann man die gegenseitige Lage von E und g einschließlich des evtl. vorhandenen Schnittpunkts S wie folgt ermitteln:
- Setze g in E ein, d.h. ersetze x1, x2 und x3 in der E-Gleichung durch die entsprechenden Zeilen aus dem g-Gleichungssystem.
- Löse die entstehende Gleichung, wenn möglich, nach λ auf und setze das Ergebnis in die g-Gleichung für λ ein.
- Fasse zu einem Vektor zusammen, das Ergebnis entspricht S.
- echt parallel, wenn das Auflösen nach λ zu einer falschen Aussage wie z.B. "0 = 1" führt.
- unecht parallel (E enthält g), wenn sich eine wahre Aussage wie z.B. "0 = 0" ergibt.
Beispiel
| = | 0 |
| = |
|
| = |
|
Überprüfe die Lage der Ebene E zu den Geraden g und h und bestimme, falls vorhanden, den jeweiligen Schnittpunkt.
Lösung siehe Video:

Lernvideo
Gegenseitige Lage von Ebene (Normalenform) und Gerade
Kanal: Mathegym