Wie bestimmt man den Limes einer Funktion, die als Summe, Differenz, Produkt oder Quotient zweier Funktionsterme ausgedrückt wird?
Handelt es sich bei f(x) um eine Summe, so kann der Limes von f(x) oft dadurch bestimmt werden, dass man den Limes der Summanden einzeln bestimmt und die Ergebnisse addiert. Geht zum Besipiel der erste Summand gegen a und der zweite gegen b, so geht f(x) gegen a+b. Sofern dabei ∞ auftritt, beachte folgende Regeln (in Anführungszeichen schreiben!):
"c + ∞" = ∞"c + (-∞)" = -∞
Soll heißen: Wenn ein Summand gegen c geht und der andere gegen ∞, dann geht f(x) gegen ∞. Zweite Zeile analog.
Genauso kann man bei Differenzen, Produkten und Quotienten verfahren. Beachte im Zusammenhang mit ∞ die Regeln:
"c − ∞" = -∞"∞ − c" = ∞
"c · ∞" = ±∞ [+ wenn c positiv; − wenn c negativ]
"∞ : c" = ±∞ [+ wenn c positiv; − wenn c negativ]
"c : ∞" = 0
KEINE Regel gibt es für folgende Fälle. Hier muss man den Term evtl. umformen, um den Limes richtig zu ermitteln:
"∞ − ∞" = ?"∞ : ∞" = ?
"0 · ∞" = ?
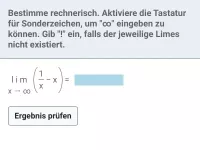
Beispiel
| = | ? |
Lösung:
| gegen -∞, also ergibt sich |
| = |
| = |
∞
Siehe auch