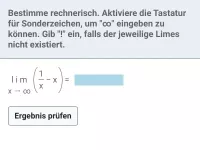
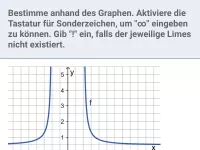
Welche drei Möglichkeiten gibt es für das Verhalten einer Funktion im Unendlichen?
Der Limes von f(x) für x → ∞ bzw. x → -∞ gibt an, wie sich die Funktion am äußeren rechten/linken Rand des Definitionsbereichs, also für "sehr, sehr große/kleine" x-Werte verhält:
| Fall | Der Funktionswert | Der Graph | Limes |
|---|---|---|---|
| Konvergenz | ...nähert sich einem Wert c an, d.h. |f(x) − c| wird beliebig klein | ...besitzt die waagrechte Asymptote y = c | = c |
| bestimmte Divergenz | ...wird beliebig groß bzw. beliebig klein, d.h. er überschreitet/unterschreitet jede noch so große/kleine Marke | ...steigt/fällt immer weiter nach oben/unten (nicht zwangsläufig monoton) | = ± ∞ |
| unbestimmte Divergenz | weder die erste noch die zweite Zeile treffen zu | existiert nicht | |
Beispiel
Bestimme aufgrund der Abbildung:
| g(x) |
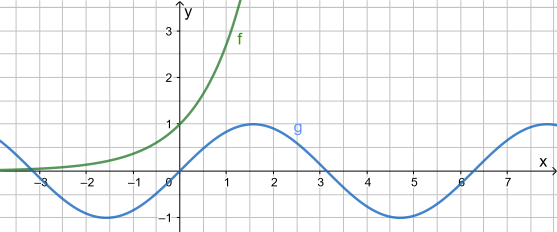
Lösung:
| f(x) = ∞ |
Begründung: y wird beliebig groß (Graph erreicht jede Höhe), wenn man nur weit genug nach rechts geht.
| f(x) = 0 |
Begründung: y unterscheidet sich von 0 beliebig wenig (Graph nähert sich der x-Achse y = 0 an), wenn man nur weit genug nach links geht.
| g(x) existiert nicht |
Begründung: weder besitzt der Graph eine waagrechte Asymptote noch "verabschiedet er sich Richtung Himmel/Hölle".
Siehe auch