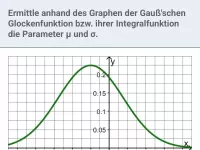
Wie lautet der Term einer Gauß'schen Glockenfunktion und wie beeinflussen μ und σ die Lage und Form ihres Graphen?


Eine Gauß'sche Glockenfunktion besitzt den in der Abbildung dargestellten Graphen und Term:
  • Lage des Graphen der Gauß'schen Glockenfunktion
μ gibt die x-Koordinate des Hochpunkts und die Lage der senkrechten Symmetrieachse an.
  • Form des Graphen der Gauß'schen Glockenfunktion
Je größer σ ist, desto "breiter" wird der Graph. σ gibt an, wie weit die Wendestellen von der Extremstelle entfernt sind. Damit die Fläche unter dem Graphen den Inhalt 1 beibehält, muss er mit zunehmender Streckung in x-Richtung entlang der y-Achse gestaucht werden.
Beispiel
Entscheide, ob der folgende Term zu einer Gauß'schen Glockenfunktion gehören kann, und ermittle gegebenenfalls passende Werte für die Parameter μ und σ:
φ
 
x
=
2
2π
·
e
−
2x
2
+
2x
−
0,5
Damit der gegebene Term mit 
φ
μ;
 
σ
 
x
=
1
σ
2π
·
e
−
x
−
μ
2
2σ
2
 übereinstimmt, kann man versuchen, durch die Wahl von σ die Vorfaktoren anzugleichen:
2
2π
=
1
σ
2π
·
2π
2
=
1
σ
Kehrwert bilden
σ
=
1
2
Mit diesem Wert von σ gilt für den Exponenten von 
φ
μ;
 
σ
 
x
:
−
x
−
μ
2
2
·
1
2
2
=
−
x
−
μ
2
1
2
=
−
2
·
x
−
μ
2
Wegen 
−
2x
2
+
2x
−
0,5
=
−
2
·
x
2
−
x
+
0,25
=
−
2
·
x
−
0,5
2
 ist Gleichheit somit gegeben für 
σ
=
1
2
 und 
μ
=
1
2
.
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.