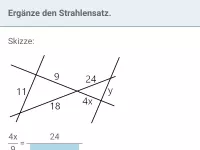
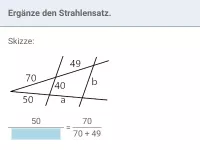
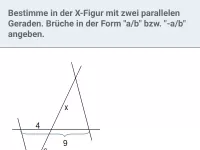
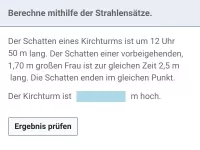
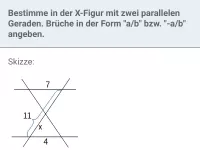
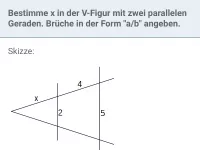
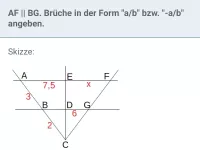
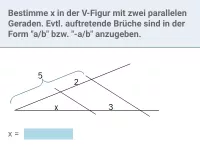
Wie kann man überprüfen, ob zwei Geraden e und f in einer V-Figur parallel sind?
Umkehrung des ersten Strahlensatzes: Um in einer "V-Figur" zu überprüfen, ob die vermeintlich parallelen Geraden wirklich parallel sind, bestimmt man bei beiden Strahlen das Verhältnis "vorderer Abschnitt" : "hinterer Abschnitt". Ist das Verhältnis gleich, so liegt Parallelität vor.
Vorsicht: sobald du die Längen der vermeintlich parallelen Strecken bei der Prüfung miteinbeziehst, kannst du nicht sicher auf Parallelität schließen (d.h. der zweite Strahlensatz ist nicht umkehrbar). Selbst wenn die Verhältnisse gleich sind, müssen also weitere Überlegungen angestellt werden.
Beispiel
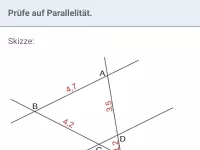
Prüfe die Geraden AD, BC und FG paarweise auf Parallelität
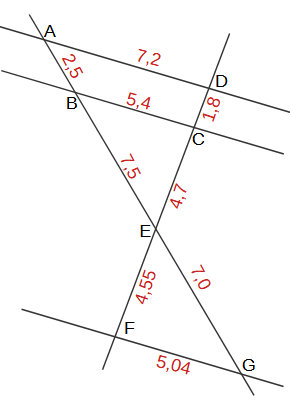
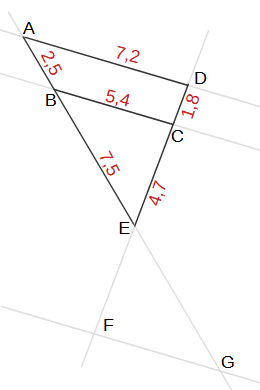
- AD und BC
Betrachte die passende V-Vigur:
| = |
| X | ||||||||
| = |
| |||||||||
| = |
| |||||||||
Parallelität beider Geraden liegt genau dann vor, wenn die Gleichung oben richtig ist. Also sind AD und BC nicht parallel.
Achtung: Hätte man die Abschnitte der parallelen Geraden für die Prüfung verwendet, hätte man zu einem Fehlschluss kommen können, denn:
| = |
| ||||||||||
| = |
| X | |||||||||
| = |
| ||||||||||
| = |
| ||||||||||
Das Beispiel zeigt, dass man die Abschnitte der parallelen Geraden NICHT verwenden kann, um Parallelität zu beweisen.
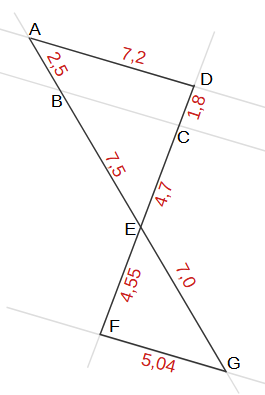
- AD und FG
Betrachte die passende X-Vigur:
| = |
| X | ||||||||||||
| = |
| |||||||||||||
| = |
| |||||||||||||
Da die Geichung stimmt sind AD und FG parallel.
- BC und FG
Da BC nicht parallel zu AD ist, kann BC auch nicht parallel zu FG sein (wenn AD || FG).
Siehe auch