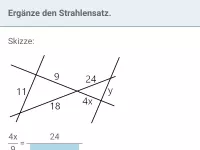
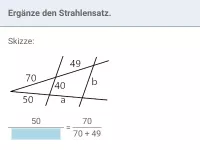
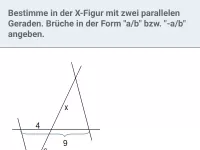
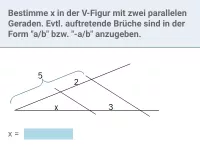
Wie lauten die Verhältnisgleichungen gemäß der Strahlensätze?
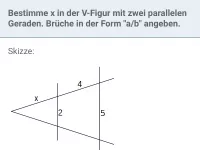
Wenn zwei sich schneidende Geraden von zwei Parallelen geschnitten werden, spricht man von einer V-Figur, wenn sie wie folgt aussieht:
Es gelten die Strahlensätze (e und f parallel):
Es gelten die Strahlensätze (e und f parallel):
1. Strahlensatz
Abschnitte der beiden Strahlen werden zueinander in Beziehung gesetzt:
a : g = c : h
a : b = c : d
2. Strahlensatz
Seitenlängen des kleinen und des großen Dreiecks werden zueinander in Beziehung gesetzt:
a : g = e : f
c : h = e : f
Beispiel 1
Skizze (nicht maßstabsgetreu):
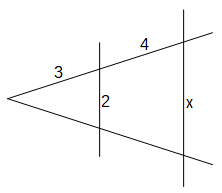
Berechne x.
Benötigt wird der 2. Strahlensatz, da hier die parallelen Seiten vorkommen.
Achtung: Beim 2. Strahlensatz kommen nur Dreiecksseiten (im kleinen und im großen Dreieck) vor. Deshalb ist der folgende Ansatz zwar bei Schülern "beliebt", aber dennoch falsch:
Falscher Ansatz:
| = |
|
Erläuterung: der Abschnitt auf dem oberen Strahl mit der Länge 4 ist keine Dreieckseite! Statt dessen muss man die beiden oberen Abschnitte
zusammen nehmen, da sie zusammen eine Seite des großen Dreiecks bilden:
|
| = |
|
| ||||||||||||||
| = |
| |||||||||||||||
Lernvideo
Strahlensatz
Kanal: Mathegym
Beispiel 2
Skizze (nicht maßstabsgetreu):
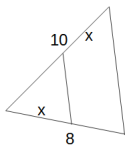
Berechne x.
Hier hilft der 1. Strahlensatz weiter, da keine Parallelen vorkommen. Allerdings benötigt man für den Ansatz noch mindestens eine Abschnittslänge, drum ergänzt man zunächst:
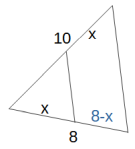
Jetzt kann man den Ansatz aufstellen und die Gleichung nach x auflösen:
| = |
|
| ||||||||||||||||||||
| = |
| |||||||||||||||||||||
| = |
|
| ||||||||||||||||||||
| = |
|
| ||||||||||||||||||||
| = |
| kürzen | ||||||||||||||||||||
| = |
| |||||||||||||||||||||

Lernvideo
Strahlensatz
Kanal: Mathegym
Siehe auch