Wie wird ein Winkel von 90° in Bogenmaß umgerechnet und wie kann man sich das Bogenmaß vorstellen?
Jeder Winkel kann in Grad angegeben werden (z.B. 90° für den rechten Winkel) oder im Bogenmaß (π/2).
Man muss sich das so vorstellen: Sticht man in den Scheitel des 90°-Winkels ein und zeichnet einen Kreis mit Radius 1, so ist der Bogen zwischen den beiden Schenkeln genau π/2 lang.
Umrechnung zwischen Grad- und Bogenmaß mittels Dreisatz, ausgehend von
180° (Grad) entspricht π (Bogenmaß)
Beispiel 1
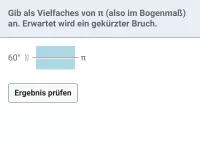
Wandle 230° ins Bogenmaß um.
| ≙ |
|
| |||||||
| ≙ |
|
| |||||||
| ≙ |
| ||||||||
Alternative Rechenwege/Darstellungen des Ergebnisses:
- Teile 230° durch 180° und multipliziere mit π.
- Ebenso könnte man auch durch 360° teilen und dann mit 2π multiplizieren.
- Man kann den Bruch natürlich auch als (gerundete) Dezimalzahl angeben, das macht dann ca. 1,28 π.
- Man kann das Bogenmaß auch nur als Zahl (ohne π-Konstante) schreiben; dazu muss man mit π multiplizieren, das ergibt ca. 4,01.
Beispiel 2
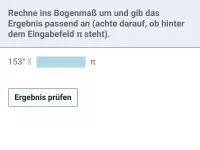
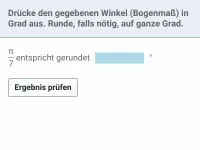
Drücke die Winkel π/11 und 5 (Bogenmaß) jeweils in Grad aus.
- Winkel π/11
| ≙ |
|
| ||||||||||
| ≙ |
| |||||||||||
| ≙ |
| |||||||||||
- Winkel 5 (Bogenmaß)
| ≙ |
|
| ||||||||
| ≙ |
|
| ||||||||
| ≙ |
| |||||||||
Bei beiden Aufgaben könnte man, alternativ, auch einfach den im Bogenmaß gegebenen Winkel durch π teilen und das Ergebnis mit 180° multiplizieren.