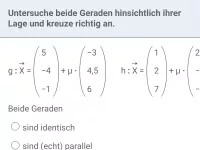
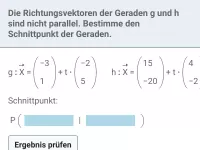
Welche Vektoren kommen in der Parameterform einer Geraden vor und welche Bedeutung haben sie?
Bei einer Gleichung in Parameterform wird der Ortsvektor zu einem Aufpunkt (Stützvektor) und ein Richtungsvektor der Geraden angegeben. Der Ortsvektor "verankert" die Gerade im Koordinatensystem, der Richtungsvektor gibt ihre Richtung vor. Weder der Orts- noch der Richtungsvektor sind eindeutig festgelegt.
Beispiel 1
| = |
|
(a) Gib für g eine andere Gleichung in Parameterform an, die weder im Ortsvektor noch im Richtungsvektor mit der Gleichung oben übereinstimmt.
(b) Gib eine Gleichung an für die Gerade h, die parallel zu g ist und durch den Punkt (1|2|-5) geht.
(c) Gib eine Gleichung an für eine Gerade i, die senkrecht zu g steht und g in einem beliebigen Punkt schneidet.)
- Lösung zu (a)
Einen alternativen Ortsvektor (Stützvektor) erhält man, indem man für μ einen beliebigen Parameterwert ≠ 0 in die Geradengleichung einsetzt, z.B. μ = 1:
| = |
|
Wenn man jetzt noch die Koordinaten des Richtungsvektors verdoppelt (oder verdreifacht...), erhält man einen alternativen, aber die gleiche Richtung vorgebenden Richtungsvektor mit den Koordinaten -2, 2 und 4. Eine mögliche Lösung für (a) lautet damit
|
- Lösung zu (b)
Der Richtungsvektor kann, da h || g, von g übernommen werden. Ein geeigneter Ortsvektor ergibt sich aus dem vorgegebenen Punkt, also
|
- Lösung zu (c)
Man benötigt lediglich einen Richtungsvektor, der zum Richtungsvektor von g senkrecht steht. Der Richtungsvekor von g hat als zweite Koordinate den Wert 1 und als dritte den Wert 2. Vertauscht man die zweite und dritte Koordinate und nimmt von einer die Gegenzahl, erhält man mit 0 als erste Koordinate einen senkrechten Vektor (gefärbt), wie man mit Hilfe des Skalarprodukts nachrechnen kann:
| = | 0 |
Verwendet man als Stützvektor (Aufpunkt) der Geraden i denselben wie bei g, so erhält man folgende Lösung für i:
| = |
|

Lernvideo
Geraden im Raum, Parameterform, Parallele und Senkrechte, Beispiel
Kanal: Mathegym
Beispiel 2
| = |
|
(a) Gib für g eine andere Gleichung in Parameterform an, die weder im Ortsvektor noch im Richtungsvektor mit der Gleichung oben übereinstimmt.
(b) Gib eine Gleichung an für die Gerade h, die parallel zu g ist und durch den Punkt (1|2|-5) geht.
- Lösung zu (a)
Einen alternativen Ortsvektor (Stützvektor) erhält man, indem man für μ einen beliebigen Parameterwert ≠ 0 in die Geradengleichung einsetzt, z.B. μ = 1:
| = |
|
Wenn man jetzt noch die Koordinaten des Richtungsvektors verdoppelt (oder verdreifacht...), erhält man einen alternativen, aber die gleiche Richtung vorgebenden Richtungsvektor mit den Koordinaten -2, 2 und 4. Eine mögliche Lösung für (a) lautet damit
|
- Lösung zu (b)
Der Richtungsvektor kann, da h || g, von g übernommen werden. Ein geeigneter Ortsvektor ergibt sich aus dem vorgegebenen Punkt, also
|
Siehe auch