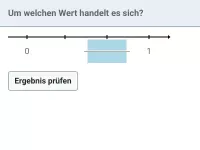
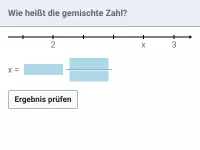
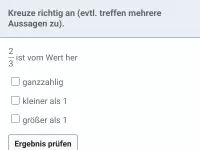
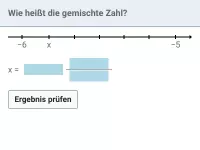
Wie vergleicht man die Größe von Brüchen anhand einfacher Regeln?

  • Haben zwei Brüche denselben Nenner, ist der Bruch größer, der den größeren Zähler besitzt.
  • Haben zwei Brüche denselben Zähler, ist der Bruch größer, der den kleineren Nenner besitzt.
  • Beträgt der Zähler mehr als die Hälfte des Nenners, so ist der Bruch größer als 1/2.
  • Beträgt der Zähler weniger als die Hälfte des Nenners, so ist der Bruch kleiner als 1/2
  • Es gilt 1/2 < 2/3 < 3/4 < 4/5 u.s.w. (bei diesen Brüchen ist der Zähler um eins kleiner als der Nenner).
Beispiel 1
Vergleiche hinsichtlich ihrer Größe:
5
31
 
und
 
7
31
7
4
 
und
 
7
3
7
8
 
und
 
8
9
6
11
 
und
 
3
7
3
20
 
und
 
2
15
5
31
 
<
 
7
31
, da beide Brüche denselben Nenner haben und der rechte Bruch den größeren Zähler.
7
4
 
<
 
7
3
, da beide Brüche denselben Zähler haben haben und der rechte Bruch den kleineren Zähler.
7
8
 
<
 
8
9
, da beim linken Bruch 
1
8
 zum Ganzen fehlt und beim rechten Bruch 
1
9
 (also weniger).
6
11
 
>
 
3
7
, da beim linken Bruch der Zähler etwas größer als die Hälfte des Nenners ist und beim rechten etwas kleiner, d.h. der linke Bruch ist größer als 
1
2
 und der rechte kleiner.
3
20
 
>
 
2
15
, da man den linken Bruch zu 
9
60
 und den rechten zu 
8
60
 erweitern kann.
BRÜCHE vergleichen Erklärung – größer oder kleiner, Brüche ordnen
Lernvideo

BRÜCHE vergleichen Erklärung – größer oder kleiner, Brüche ordnen

Kanal: MathemaTrick
Beispiel 2
Vergleiche hinsichtlich ihrer Größe:
4
3
11
 
und 3
17
10
Lösung:
4
3
11
47
11
<
3
17
10
47
10
gleicher Zähler, 10
<
11
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen