Welche Vorzeichenverläufe kann f´ in der Umgebung einer Nullstelle bei x_0 haben und wie lassen sich diese graphisch interpretieren?
Ist f in einer Umgebung von x0 differenzierbar und besitzt Gf an der Stelle x0 eine waagrechte Tangente, d.h. also f ´ (x0) = 0, so befindet sich dort entweder ein Hoch-, ein Tief- oder ein Terrassenpunkt. Was genau, verrät der Vorzeichenverlauf von f ´: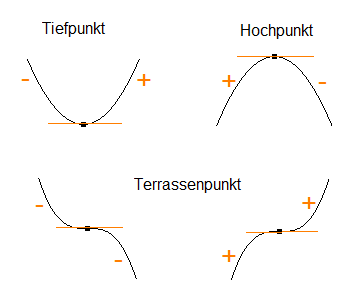
- "−,0,+" bedeutet für Gf "fallend,waagrecht,steigend", also Tiefpunkt (relatives Minimum von f)
- "+,0,−" bedeutet für Gf "steigend,waagrecht,fallend", also Hochpunkt (relatives Maximum von f)
- "−,0,−" bedeutet für Gf "fallend,waagrecht,fallend", also Terrassenpunkt
- "+,0,+" bedeutet für Gf "steigend,waagrecht,steigend", also ebenfalls Terrassenpunkt

Beispiel 1
Bestimme für die in ganz ℝ definierte ganzrationale Funktion f mit
sämtliche Extrempunkte mithilfe des Vorzeichwechselkriteriums der ersten Ableitung.
| = |
|
Lösung siehe Video (letztes Beispiel)

Lernvideo
EXTREMA Vorzeichenwechsel Kriterium – Hochpunkt Tiefpunkt berechnen
Kanal: MathemaTrick
Beispiel 2
Schließe aus der Vorzeichentabelle von f´ auf evtl. Hoch-, Tief- und Terrassenpunkte von Gf.
|
|
|
|
|
|
| |||||||||||||
|
|
|
|
|
|
An den Stellen
und
ist die Ableitung jeweils 0, d.h. der Graph besitzt dort eine waagrechte Tangente. Nun muss man den jeweiligen Vorzeichenverlauf betrachten, um zu wissen, ob es sich um lokale Extremstellen oder um Terrassenstellen handelt.
x | = | 0 |
x | = | 3 |
An der Stelle
wechselt die Ableitung ihr Vorzeichen von Minus zu Plus, d.h. der Graph geht von "fallend" in "steigend" über und damit liegt dort ein Tiefpunkt vor.
x | = | 0 |
An der Stelle
wechselt die Ableitung ihr Vorzeichen nicht, also liegt dort ein Terrassenpunkt vor.
x | = | 3 |
Siehe auch






