Was ist ein Randextremum und bei welchem Funktionstyp tritt es auf?
Besitzt eine Funktion mit Wurzelterm eine Definitionsmenge, die an einer bestimmten Stelle beginnt oder endet, liegt dort immer ein so genanntes Randextremum vor. Der zugehörige Graph besitzt dort einen Extrempunkt, an dem die zugehörige Tangente nicht unbedingt waagrecht verlaufen muss. Die Art des Extremums kann z.B. anhand des Vorzeichens der Ableitung in der Umgebung bestimmt werden.
Beispiel
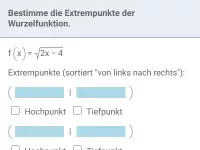
Bestimme alle Extrempunkte des Graphen der Funktion
| = |
|
- Bestimmung der Definitionsmenge
Der Radikand darf nicht negativ sein, also
und somit
| 0 |
|
|
Die Definitionsmenge lautet somit D = [2,5; +∞[.
- Extremstellen im Inneren des Definitionsbereichs
Mithilfe der Kettenregel ergibt sich
| = |
|
Da die Ableitungsfunktion nie den Wert Null annimmt, besitzt der Graph keine Punkte mit waagrechter Tangente und somit keine Extrempunkte im Inneren des Definitionsbereichs.
- Extremstellen am Rand des Definitionsbereichs
An der Stelle
muss hingegen ein Randextremum vorliegen. Wegen
für
steigt der Graph in der Umgebung und es liegt ein Tiefpunkt vor.
x | = | 2,5 |
| 0 |
| 2,5 |
Aus
folgt:
| = | 3 |
Tiefpunkt: (2,5 | 3)
Siehe auch