Monotonie und relative Extrempunkte, Matheübungen

Bestimmung von Monotonieintervallen sowie relativen Extrema (Hoch- und Tiefpunkte) mit Hilfe der Ableitungsfunktion - Lehrplan für 12. Klasse

Hilfe

  • Eine Funktion f ist in einem Intervall streng monton steigend, wenn für zwei unterschiedliche Werte a und b aus diesem Intervall mit a<b stets gilt f(a)<f(b).

    Eine Funktion f ist in einem Intervall streng monton fallend, wenn für zwei unterschiedliche Werte a und b aus diesem Intervall mit a<b stets gilt f(a)>f(b).

    Mit Monotonieintervall ist jeweils das größtmögliche Intervall innerhalb von Df gemeint, in dem eine strenge Monotonie vorliegt.

Skizziere den Graphen der Funktion im maximalen Definitionsbereich und ermittle die Monotonieintervalle.

  • f
     
    x
    =
    1
    x
    −
    3
    G
    f
     fällt streng monoton für
     
    x ∈ ℝ\{3}
       
     
    x
     
    <
     
    1
       
     
    x
     
    >
     
    1
       
     
    x
     
    <
     
    3
       
     
    x
     
    >
     
    3
    G
    f
     steigt streng monoton für
     
    x ∈ ℝ\{3}
       
     
    x
     
    <
     
    1
       
     
    x
     
    >
     
    1
       
     
    x
     
    <
     
    3
       
     
    x
     
    >
     
    3
    Notizfeld
    Notizfeld
    Tastatur
    Tastatur für Sonderzeichen
    Kein Textfeld ausgewählt! Bitte in das Textfeld klicken, in das die Zeichen eingegeben werden sollen.
keine Berechtigung
Was bedeutet "streng monoton steigend/fallend" bei Funktionen?
#1135

Eine Funktion f ist in einem Intervall streng monton steigend, wenn für zwei unterschiedliche Werte a und b aus diesem Intervall mit a<b stets gilt f(a)<f(b).

Eine Funktion f ist in einem Intervall streng monton fallend, wenn für zwei unterschiedliche Werte a und b aus diesem Intervall mit a<b stets gilt f(a)>f(b).

Mit Monotonieintervall ist jeweils das größtmögliche Intervall innerhalb von Df gemeint, in dem eine strenge Monotonie vorliegt.

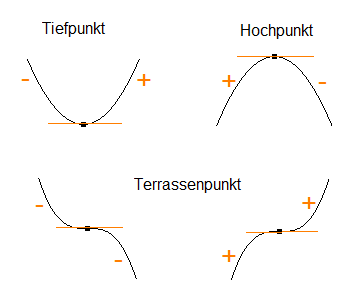
Welche Vorzeichenverläufe kann f´ in der Umgebung einer Nullstelle bei x_0 haben und wie lassen sich diese graphisch interpretieren?
#473
Ist f in einer Umgebung von x0 differenzierbar und besitzt Gf an der Stelle x0 eine waagrechte Tangente, d.h. also f ´ (x0) = 0, so befindet sich dort entweder ein Hoch-, ein Tief- oder ein Terrassenpunkt. Was genau, verrät der Vorzeichenverlauf von f ´:
  • "−,0,+" bedeutet für Gf "fallend,waagrecht,steigend", also Tiefpunkt (relatives Minimum von f)
  • "+,0,−" bedeutet für Gf "steigend,waagrecht,fallend", also Hochpunkt (relatives Maximum von f)
  • "−,0,−" bedeutet für Gf "fallend,waagrecht,fallend", also Terrassenpunkt
  • "+,0,+" bedeutet für Gf "steigend,waagrecht,steigend", also ebenfalls Terrassenpunkt
Beispiel 1
Schließe aus der Vorzeichentabelle von f´ auf evtl. Hoch-, Tief- und Terrassenpunkte von Gf.
x <
0
< x <
3
< x
f ´
 
x
−
0
+
0
+
Beispiel 2
Bestimme für die in ganz ℝ definierte ganzrationale Funktion f mit 
f
 
x
=
2x
3
−
3x
2
−
1
 sämtliche Extrempunkte mithilfe des Vorzeichwechselkriteriums der ersten Ableitung.
Was zeigt das Vorzeichen der Ableitung f'(x) einer Funktion an?
#400

Die Ableitung f´ einer differenzierbaren Funktion f liefert für jede definierte Stelle x die lokale Änderungsrate (= Steigung des Graphen von f an dieser Stelle). Insbesondere zeigt das Vorzeichen von f´ an, ob f im betrachteten Intervall zunimmt oder abnimmt:

f´(x) f bzw. Gf
> 0 streng monoton zunehmend bzw. wachsend
< 0 streng monoton abnehmend bzw. fallend
= 0 waagrechte Tangente

Achtung: die Tabelle ist von links nach rechts zu lesen, d.h. aus f´(x)>0 in einem bestimmten Intervall kann auf strenge Monotonie von f geschlossen werden - aber nicht umgekehrt. Wenn f in einem bestimmten Intervall streng monoton wächst, kann es dort durchaus einzelne Stellen geben, an denen die Ableitung gleich null ist (waagrechte Tangente).

Beispiel
Bestimme die Monotonieintervalle der ganzrationalen Funktion f aufgrund der gegebenen ersten Ableitung.
f ´
 
x
=
−
1
3
·
x
3
·
x
+
5
Wie bestimmt man rechnerisch lokale Maxima und Minima einer Funktion?
#698

Bestimmung der lokalen Maxima und Minima einer Funktion:

  1. Bestimme die Nullstellen der ersten Ableitung der Funktion.
  2. Überprüfe mithilfe des Vorzeichenwechsel-Kriteriums, ob im Graph ein Hoch- oder Tiefpunkt vorliegt.

Randextrema:

Untersuche, ob an den Intervallgrenzen lokale Maxima oder Minima vorliegen. Bestimme dazu den Funktionswert an den Intervallgrenzen und überprüfe, ob die erste Ableitung an den Intervallgrenzen größer oder kleiner als Null ist:
  • linker Rand: f'(x)<0, Randmaximum
  • linker Rand: f'(x)>0, Randminimum
  • rechter Rand: f'(x)<0, Randminimum
  • rechter Rand: f'(x)>0, Randmaximum

Bestimmung des globalen Maximums und Minimums:

  1. Der größte Wert der lokalen Maxima und Randmaxima wird als globales Maximum bezeichnet.
  2. Der kleinste Wert der lokalen Minima und Randminima wird als globales Minimum bezeichnet.
698