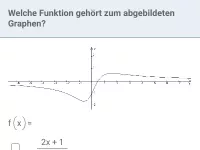
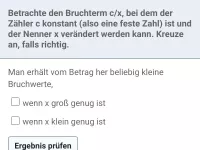
Wie entwickelt sich der Wert eines Bruchs, wenn der Nenner (bei konstantem Zähler) größer bzw. kleiner wird?
Brüche kann man als Teilung auffassen: Der Zählerwert wird durch den Nennerwert geteilt. Der Bruchwert ist demnach betragsmäßig umso größer
- je größer der Zählerbetrag (bei konstantem Nenner) oder
- je kleiner der Nennerbetrag (bei konstantem Zähler) ist.
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Wie lautet die korrekte Schreibweise dafür, dass für x alle rationalen Zahlen mit Ausnahme bestimmter Werte zugelassen sind (Definitionsmenge)?
- Wo liegen die Quadranten 1-4 im Koordinatensystem?
- Die Asymptoten einer gebrochen-rationalen Funktion liefern Anhaltspunkte für den Verlauf des Grafen - warum reichen sie aber für eine zutreffende Skizze nicht aus?