Erkläre Zweck und Aufbau eines Prozessdiagramms.
Stochastische Prozesse
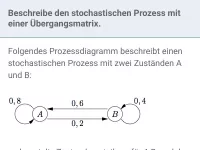
Zufallsvorgänge mit endlich vielen Zuständen lassen sich grafisch durch Prozessdiagramme darstellen.
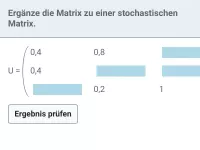
- Ein Endzustand heißt absorbierend und wird am Ringpfeil mit der Übergangswahrscheinlichkeit 100% =1 erkannt.
- Alle anderen Zustände sind innere Zustände. Bei diesen ist die Summe der Wahrscheinlichkeiten aller abgehenden Pfeile gleich 1 (sofern im Diagramm ALLE möglichen Zustände berücksichtigt werden).
Die Zustandsverteilung fasst zusammen, mit welchen Wahrscheinlichkeiten die verschiedenen Zustände zu einem bestimmten Zeitpunkt besetzt sind.
Der stochastische Prozess umfasst die Folge der Zustandsverteilungen eines Prozessdiagramms.
Beispiel 1
Zur Vorbereitung auf das Abitur gibt es Aufgaben in den Schwierigkeitsstufen 1 (leicht) bis 3 (schwer). Ein Schüler startet mit den einfachsten Aufgaben und übt, bis er Level 3 erreicht hat. Den Übergang von Level 1 nach Level 2 schafft er mit 70% Wahrscheinlichkeit, den Übergang von Level 2 nach Level 3 mit 35% Wahrscheinlichkeit. Erstelle ein Prozessdiagramm.
Lösung:
- Schritt 1: Zustände ermitteln
Es geht hier um das Arbeiten auf Level 1, 2 und 3, was man als Zustände des Prozesses bezeichnen kann:
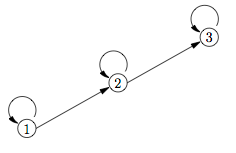
- Schritt 2: Übergangswahrscheinlichkeiten eintragen
Mit den gegebenen Übergangswahrscheinlichkeiten von Level 1 nach 2 bzw. Level 2 nach 3 vervollständigt sich das Diagramm zu:
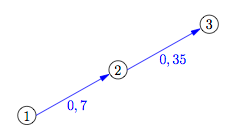
- Schritt 3: Die restlichen Übergangswahrscheinlichkeiten ermitteln
In jedem Zustand ist die Summe der Wahrscheinlichkeiten an abgehenden Pfeilen gleich 1. Konkret bedeutet dies: ein Schüler startet mit Level 1-Aufgaben. Entweder er steigt nun auf zu Level 2 (Wahrscheinlichkeit 70%) oder er übt weiter auf Level 1 (Restwahrscheinlichkeit 30%). Mehr Optionen gibt es am Anfang des Übungsprozesses nicht.
Bei Level 2 verfährt der Schüler genauso: er steigt auf (35%) oder er übt weiter (65%).
Im Endstadium verbleibt der Schüler, dies bedeutet: wenn der Schüler mal das höchste Level erreicht hat, wird er nur noch schwierige Aufgaben üben. Daher ist dort die Wahrscheinlichkeit 1 einzutragen.
Damit vervollständigt sich das Prozessdiagramm zu:
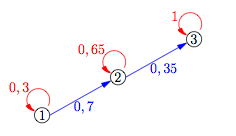
Bemerkung: Gäbe es zusätzlich auch noch Aufgaben auf einem vierten Schwierigkeitsniveau, welches 10% der Level 3-Schüler erreichen, könnte das Prozessdiagramm erweitert werden. Interessiert jedoch nur, wann wie viele Schüler im Level 3 angekommen sind, könnte das Prozessdiagramm auch unvollständig bleiben. In diesem Fall wäre die Summe aller von Level 3 abgehenden Pfeile NICHT 1 und das Prozessdiagramm sähe folgendermaßen aus:
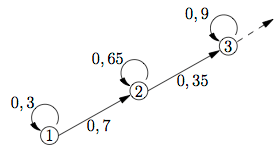
Beispiel 2
Zur Vorbereitung auf das Abitur gibt es Aufgaben in den Schwierigkeitsstufen 1 (leicht) bis 3 (schwer). Alle Schüler starten mit den einfachsten Aufgaben und üben, bis sie Level 3 erreicht haben. Den Übergang von Level 1 nach Level 2 schaffen sie durchschnittlich mit 70% Wahrscheinlichkeit, den Übergang von Level 2 nach Level 3 mit 35% Wahrscheinlichkeit. Bestimme die Zustandsverteilung nachdem drei Aufgaben geübt wurden.
Lösung:
- Schritt 1: Startverteilung ermitteln
Die Wahrscheinlichkeiten, mit denen sich die Schüler nach k Übungsschritten in den Leveln 1, 2 und 3 befinden, werden mit ak (Level 1), bk (Level 2) bzw. ck (Level 3) bezeichnet.
Da alle Schüler (100% = 1) mit den einfachsten Aufgaben starten, ist die Startverteilung (k=0) gegeben durch:
| = | 1 |
| = | 0 |
| = | 0 |
Für die weiteren Berechnungen werden aus dem Prozessdiagramm die Übergangswahrscheinlichkeiten abgelesen. Grün bezeichnet alle in Level 1 verbleibenden Wege. Blau sind alle zu Level 2 aufsteigenden bzw. in Level 2 verbleibenden Wege. Rot sind alle zu Level 3 aufsteigenden bzw. in Level 3 verbleibenden Wege.
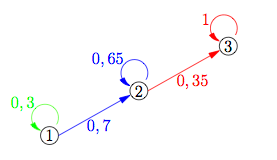
Eine neue Zustandsverteilung kann aus der vorherigen folgendermaßen berechnet werden:
| = |
|
Begründung (grüner Pfeil):
| verbleiben bei den einfachsten Aufgaben im Level 1. |
Kein Schüler fällt aus einem höheren Übungsniveau zurück zu Level 1.
| = |
|
Begründung (blaue Pfeile):
| steigen auf. |
| verbleiben auf diesem Aufgabenniveau. |
Keiner fällt von der obersten Stufe wieder herab.
| = |
|
Begründung (rote Pfeile):
| steigen auf. |
| verbleiben auf diesem Aufgabenniveau. |
Keiner kann direkt von Level 1 auf Level 3 aufsteigen, daher ist die Wahrscheinlichkeit dort 0.
- Schritt 2: Zustandsverteilung nach erstem Übungsschritt
| = | 0,3 |
| = | 0,7 |
| = | 0 |
Bedeutung: Nach dem ersten Übungsschritt bleiben 30% der Schüler auf Level 1, 70% der Schüler haben Level 2 erreicht.
- Schritt 3: Zustandsverteilung nach zweitem Übungsschritt
| = | 0,09 |
| = | 0,665 |
| = | 0,245 |
Bedeutung: Nach dem zweiten Übungsschritt sind nur noch 9% der Schüler auf Level 1, 66,5% der Schüler haben Level 2 erreicht und 24,5% der Schüler sind sogar schon in Level 3.
- Schritt 4: Zustandsverteilung nach drittem Übungsschritt
| = | 0,027 |
| = | 0,49525 |
| = | 0,47775 |
Bedeutung: Nach drei Übungsaufgaben befinden sich nur noch 2,7% der Schüler auf Level 1. Fast die Hälfte (49,5%) übt in Level 2 und auch immerhin knapp 47,8% der Schüler haben das höchste Übungslevel erreicht.