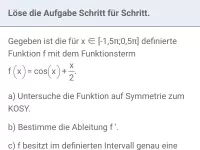
Wie lauten die Ableitungen der Funktionen sin(x) und cos(x)?
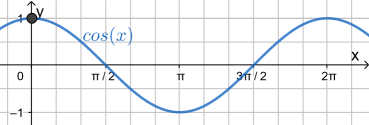
f (x) = sin(x) ⇒ f ´ (x) = cos(x)
f (x) = cos(x) ⇒ f ´ (x) = -sin(x)
f (x) = cos(x) ⇒ f ´ (x) = -sin(x)
Beispiel
| = |
|
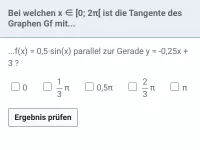
Bei welchen ist die Tangente des Graphen
parallel zur Gerade durch die Punkte (0|−1) und (1|-3)
x ∈ [0; 2π[
G | f |
| = |
|
Dieser Term muss mit der Steigung der Geraden, also
, gleichgesetzt werden:
| = | −2 |
| = |
|
| |||||||||||||||||||||
| = |
| ||||||||||||||||||||||
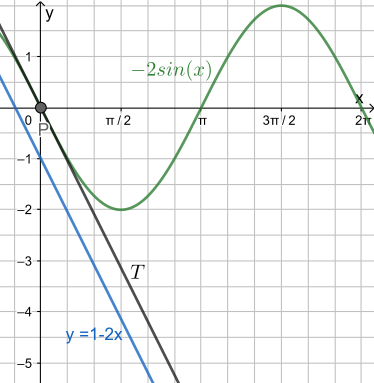
Wie man oben sieht, gibt es für diese Gleichung im Intervall [0;2π[ nur eine Lösung, nämlich
x | = | 0. |
!!! Achtung: wäre die rechte Intervallgrenze nicht ausgeschlossen (d.h. bei [0;2π]) müsste man noch
als zweite Lösung angeben !!!
x | = | 2π |
Fazit: Der Graph von f besitzt im Intervall [0;2π[ eine Tangente, die zur vorgegebenen Gerade parallel ist und zwar an der Stelle
x | = |
|
Nur zur Veranschaulichung (Graph war nicht verlangt):