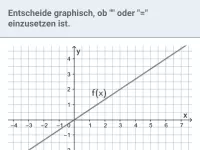
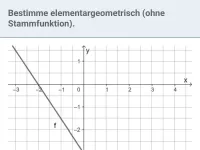
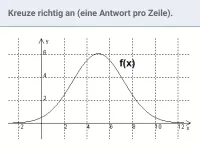
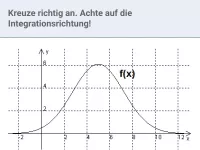
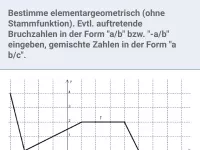
Wie kann man die Fläche zwischen dem Graphen einer positiven Funktion und der x-Achse in einem Intervall abschätzen und welche Fachbegriffe sind dabei relevant?
Die Fläche A zwischen dem Graphen einer positiven Funktion und der x-Achse in einem Intervall [a;b] kann durch Unter- und Obersumme (Un bzw. On) abgeschätzt werden (Streifenmethode).
- Die Untersumme setzt sich aus n gleichbreiten, auf der x-Achse nebeneinander stehenden Rechtecksflächen (Streifen) zusammen, die möglichst hoch sind, den Graph aber niemals überragen.
- Die Streifen der Obersumme sind möglichst niedrig, aber nie unterhalb des Graphen.
- Die Breite der Streifen beträgt in beiden Fällen (b − a)/n.
Un ≤ A ≤ On
Beispiel
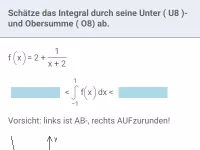
Schätze mit Hilfe der Streifenmethode (n=6) ab:
|
|
Lösung siehe Video; im zweiten Video wird ein anderes Beispiel durchgerechnet.
Lernvideo
Streifenmethode, Beispiel
Kanal: Mathegym

Lernvideo
Untersumme Obersumme berechnen – Rechtecksummen Integral
Kanal: MathemaTrick
Siehe auch