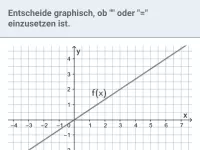
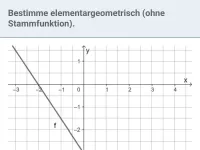
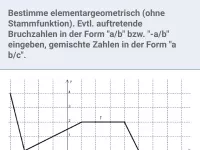
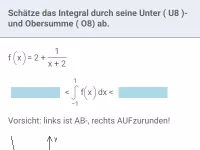
Was ist eine Integralfunktion und welche Eigenschaften hat sie?

Integriert man f(t) von a bis x (d.h. die obere Grenze ist variabel), so erhält man eine Integralfunktion I_a die jedem Wert x (= obere Grenze) das entsprechende Integral (Flächenbilanz) zuordnet. I_a besitzt im Allgemeinen folgende Eigenschaften:

mindestens eine Nullstelle x = a (weil das Integral von a bis a immer 0 ist)
sie ist Stammfunktion von f (Hauptsatz der Differential- und Integralrechnung)

Beispiel

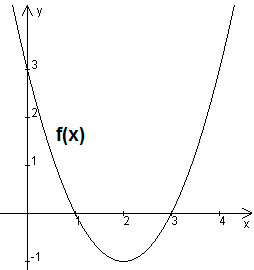
\(I(x)=\int_{0}^{x}f(t)\,dt\)

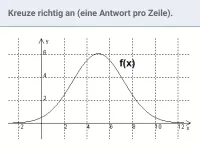
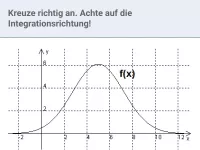
Welche Aussage ist richtig, welche falsch?

\(I\) ist im Intervall \( [3;+\infty[ \) streng monoton zunehmend.
\(I\) ist im Intervall \( [0;2]\) streng monoton abnehmend.
\(I\) ist im Intervall \( [0;2]\) nicht negativ.
\(I\) hat die stärkste Zunahme bei \(x=2\).
\(I\) besitzt ein relatives Maximum bei \(x=1\).

Richtig sind die Aussagen 1, 3 und 5.

Erklärung: Die Integralfunktion \(I(x)=\int_{0}^{x}f(t)\,dt\) gibt die Flächenbilanz zwischen dem Graphen von \(f\) und der \(x\text{-Achse}\) im Intervall \([0;x]\) an. Flächen oberhalb der \(x\text{-Achse}\) gehen positiv, Flächen unterhalb negativ in die Bilanz ein.

Für \(x>3\) ist die Fläche positiv \(\rightarrow\) \(I\) nimmt zu \(\rightarrow\) Aussage 1 ist richtig.
Für \(x<1\) ist die Fläche positiv \(\rightarrow\) \(I\) nimmt zu \(\rightarrow\) Aussage 2 ist falsch.
Für \(x\in[0;1]\) ist die Fläche positiv und für \(x \in ]1;2]\) ist die Fläche zwar negativ, aber kleiner als die Fläche im Intervall \([0;1[\text{,}\) d.h. die Flächenbilanz ist positiv \(\rightarrow\) \(I\) ist positiv \(\rightarrow\) Aussage 3 ist richtig.
Bei \(x=2\) hat \(f\) den kleinsten Funktionswert \(\rightarrow\) \(I\) hat die stärkste Abnahme \(\rightarrow\) Aussage 4 ist falsch.
Die Fläche ist für \(x<1\) positiv und für \(x\in[1;3]\) negativ \(\rightarrow\) \(I\) nimmt für \(x<1\) zu, dann ab \(\rightarrow\) Aussage 5 ist richtig.