Wie addiert oder subtrahiert man gleichartige Terme und gib Beispiele an.
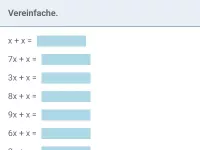
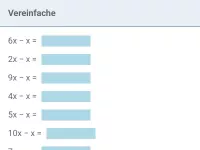
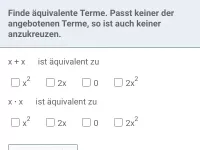
Gleichartige Terme wie z.B. 3x und -7x oder ab und 0,5ab werden addiert/subtrahiert, indem man ihre Vorzahlen addiert/subtrahiert und die (in beiden Termen vorkommenden) Variablen beibehält.
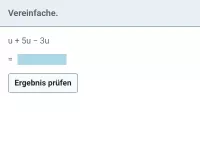
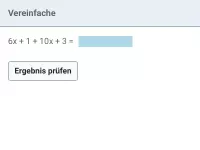
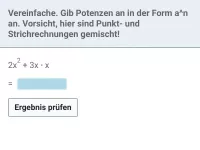
Beispiel 1
| = |
|
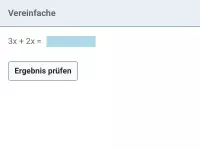
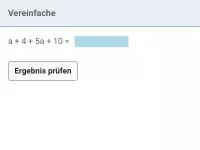
Beispiel 2
Überprüfe auf Äquivalenz:
|
|
- Vereinfachung des ersten Terms
| = |
| = |
| z |
- Vereinfachung des zweiten Terms
| = |
| = |
| = |
| z |
Die beiden Terme sind also äquivalent.
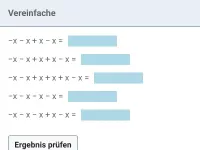
Beispiel 3
| = | ? |
| + |
|
= |
|
Erläuterung: Es treten zwei Paare gleichartiger Terme auf, die jeweils zusammengefasst werden können:
und
. Dagegen ist der
-Term zu keinem der anderen gleichartig. Daher kann er nicht mit anderen Teiltermen zusammengefasst werden und bleibt so stehen.
| = |
|
| = |
|
3c | 2 |
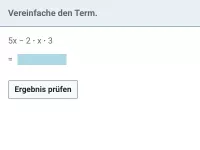
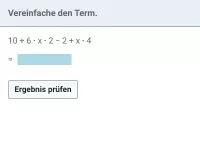
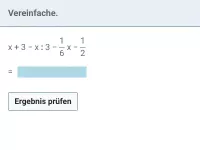
Beispiel 4
Vereinfache:
|
|
Lösung:
|
|
= |
|
|
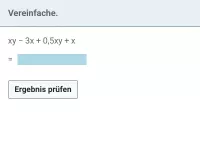
Erläuterung: es kommen zwei Summanden mit x, zwei Summanden mit y, zwei konstante Summanden (ohne Variable) sowie ein Summand mit xy vor. Die x- und die y-Summanden können jeweils zusammengefasst werden, ebenso die beiden konstanten Summanden. Der xy-Summand dagegen bleibt unverändert.
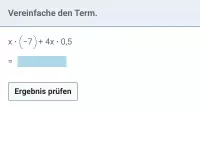
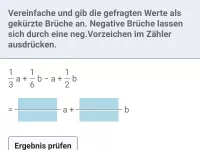
Beispiel 5
Vereinfache.
|
|
Lösung:
|
|
|
| = |
| x-Terme zusammenfassen | |||||||||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||||||||||
|
| = |
| y-Terme zusammenfassen | |||||||||||||||||||||||||||||||
|
| = |
| Zahlenterme zusammenfassen | |||||||||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||||||||||
Dieses und andere Beispiele werden in folgendem Video behandelt.

Lernvideo
Termvereinfachung Level 1
Kanal: Mathegym Basics
Siehe auch