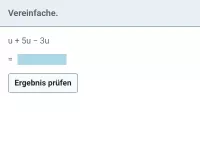
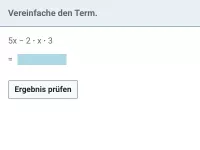
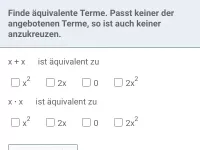
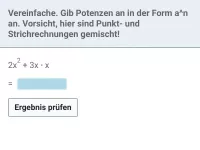
Wann sind zwei Terme als äquivalent zu betrachten?

Zwei Terme T1 und T2 sind äquivalent, wenn sie (salopp ausgedrückt) "eigentlich gleich" sind, korrekt: wenn sie die gleiche Grundmenge haben und wenn jede Zahl daraus, eingesetzt in beide Terme, zum selben Termwert führt. Man zeigt die Äquivalenz zweier Terme meistens durch Äquivalenzumformung.
Beispiel
Finde heraus, ob die folgenden Terme jeweils äquivalent sind:
(a) 
1
2
 
z
2
·
4z
   und   
z
·
z
·
2z
(b) 
z
3
+
z
   und   
z
−
2
3
·
z
Lösung durch Äquivalenzumformung:
(a)
1
2
 
z
2
·
4z
=
1
2
·
4
·
z
2
·
z
=
2
·
z
3
z
·
z
·
2z
=
2
·
z
3
Beide Terme sind äquivalent.
(b)
z
3
+
z
=
1
3
 
z
+
1z
=
4
3
·
z
z
−
2
3
·
z
=
1z
−
2
3
 
z
=
1
3
·
z
Beide Terme sind nicht äquivalent.
Ähnliche Termvereinfachungen in folgendem Video:
TERME VEREINFACHEN einfach erklärt – Rechenregeln mit Variablen, viele Beispiele
Lernvideo

TERME VEREINFACHEN einfach erklärt – Rechenregeln mit Variablen, viele Beispiele

Kanal: MathemaTrick
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen