Wie löst man zwei eingeklammerte Terme auf, die jeweils nur Plusrechnungen enthalten und miteinander multipliziert werden?

Beim Multiplizieren zweier Summen muss jeder Summand der ersten Klammer mit jedem Summanden der zweiten Klammer multipliziert werden (ergibt sich aus dem Distributivgesetz):

(a + b) · (c + d) = ac + ad + bc + bd

Beispiel 1
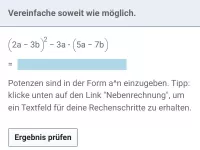
Multipliziere aus und vereinfache:
2
5
 
uv
−
2
3
·
15u
2
+
1
−
uv
- - - - - - - - - - - - - - - - - Tipp: Klammern vorher in Summen umwandeln:
2
5
 
uv
 
+
 
−
2
3
·
15u
2
 
+
 
1
 
+
 
−
uv
=
- - - - - - - - - - - - - - - - - "jeder mit jedem":
2
5
 
uv
·
15u
2
6u
3
v
+
2
5
 
uv
·
1
2
5
 
uv
+
2
5
 
uv
·
−
uv
−
2
5
 
u
2
v
2
+
−
2
3
·
15u
2
−
10u
2
+
−
2
3
·
1
−
2
3
+
−
2
3
·
−
uv
2
3
 
uv
=
- - - - - - - - - - - - - - - - - Zusammenfassen gleichartiger Terme:
6u
3
v
+
6
15
 
uv
+
10
15
 
uv
−
2
5
 
u
2
v
2
−
10u
2
−
2
3
=
6u
3
v
+
1
1
15
 
uv
−
2
5
 
u
2
v
2
−
10u
2
−
2
3
Beispiel 2
b
−
2
3
 
b
·
6a
·
a
−
30%
+
1
2
 
a
2
·
b
−
4ab
−
ab
2
Lösung siehe Video:
Distributivgesetz, Termvereinfachung, Beispiel 2
Lernvideo

Distributivgesetz, Termvereinfachung, Beispiel 2

Kanal: Mathegym
Beispiel 3
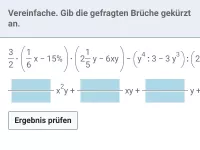
Multipliziere aus und vereinfache:
a) 
x
+
3
·
4
−
5x
b) 
−
10
−
a
·
−
7
+
b
c) 
x
2
−
1
−
2
3
 
a
·
3x
−
1
2
a)
x
+
3
·
4
−
5x
=
x
·
4
4x
+
x
·
−
5x
−
5x
2
+
3
·
4
12
+
3
·
−
5x
−
15x
=
4x
−
15x
−
11x
−
5x
2
+
12
=
−
11x
−
5x
2
+
12
b)
−
10
−
a
·
−
7
+
b
=
−
10
·
−
7
70
·
−
10
·
b
−
10b
+
−
a
·
−
7
7a
+
−
a
·
b
−
ab
=
70
−
10b
+
7a
−
ab
c)
x
2
−
1
−
2
3
 
a
·
3x
−
1
2
=
x
2
·
3x
3x
3
+
x
2
·
−
1
2
−
1
2
 
x
2
+
−
1
·
3x
−
3x
+
−
1
·
−
1
2
1
2
+
−
2
3
 
a
·
3x
−
2ax
+
−
2
3
 
a
·
−
1
2
1
3
 
a
=
3x
3
−
1
2
 
x
2
−
3x
+
1
2
−
2ax
+
1
3
 
a
2 KLAMMERN ausmultiplizieren – Klammer mal Klammer auflösen mit x, Terme vereinfachen
Lernvideo

2 KLAMMERN ausmultiplizieren – Klammer mal Klammer auflösen mit x, Terme vereinfachen

Kanal: MathemaTrick
Beispiel 4
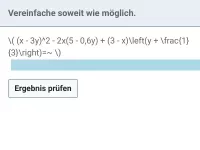
Vereinfache.
7x
−
3x
−
y
·
9y
+
x
−
1
7x
−
3x
−
y
·
9y
+
x
−
1
=
7x
−
27xy
+
3x
2
−
3x
−
9y
2
−
xy
+
y
=
7x
−
27xy
−
3x
2
+
3x
+
9y
2
+
xy
−
y
=
7x
+
3x
10x
 
−
27xy
+
xy
−
26xy
−
3x
2
+
9y
2
−
y
=
10x
−
26xy
−
3x
2
+
9y
2
−
y
Beachte: die Klammer in der zweiten Zeile wird gerne vergessen!
Klammern auflösen Level 3
Lernvideo

Klammern auflösen Level 3

Kanal: Mathegym Basics
Beispiel 5
Multipliziere die Klammern aus und vereinfache. \[ (a^2 - x)(2a + 5)(x - 3) \]
\[ \left. \begin{aligned}[t] \text{Klammern 1 und 2 multiplizieren:}\\ \underbrace{(a^2 - x)(2a + 5)}_{\text{ausmultiplizieren}}\,(x - 3) \\[6pt] \text{Man erhält:}\\ \underbrace{(2a^3 + 5a^2 - 2ax - 5x)(x - 3)}_{\text{ausmultiplizieren}} \\[6pt] \text{Multiplizieren mit Klammer 3:}\\ 2a^3x + 5a^2x - 2ax^2 - 5x^2 - 6a^3 - 15a^2 + 6ax + 15x \end{aligned} \right. \] Es kann nicht mehr weiter vereinfacht werden. Im Video wird der Lösungsweg ausführlich erläutert.
3 KLAMMERN ausmultiplizieren – drei Klammern miteinander multiplizieren
Lernvideo

3 KLAMMERN ausmultiplizieren – drei Klammern miteinander multiplizieren

Kanal: MathemaTrick
Beispiel 6
Multipliziere aus und vereinfache so weit wie möglich! \[2x(3-2x)(3x+3)\]
\[ \begin{aligned} \text{Zuerst den Faktor mit einer Klammer multiplizieren:}\\ \underbrace{2x(3-2x)}_{6x-4x^2}(3x+3) \\[10pt] \text{Dann die beiden Klammern multiplizieren:}\\ (6x-4x^2)(3x+3)= \\ \underbrace{6x \cdot 3x}_{18x^2} + \underbrace{6x \cdot 3}_{18x} - \underbrace{4x^2 \cdot 3x}_{12x^3} - \underbrace{4x^2 \cdot 3}_{12x^2}= \\[10pt] \text{Gleichartige Terme zusammenfassen:}\\ \color{blue}{18x^2} \color{orange}{+18x} \color{green}{-12x^3} \color{blue}{-12x^2} = \\ \color{green}{-12x^3} \color{blue}{+6x^2} \color{orange}{+18x} \end{aligned} \] Tipp: Multipliziere immer zuerst den Faktor mit einer der Klammern - auch wenn er nicht gleich am Anfang steht. So musst Du erst im letzten Schritt zusammenfassen. Wegen des Kommutativgesetzes bei Multiplikation ist das erlaubt.
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen