Was sind die drei binomischen Formeln und wofür werden sie verwendet?

Die drei Binomischen Formeln (BF) lauten:

  1. (a + b)² = a² + 2ab + b²
  2. (a − b)² = a² − 2ab + b²
  3. (a + b) (a − b) = a² − b²
In dieser Richtung (links mit Klammer, rechts ohne) dienen die Formeln dazu, Klammern schneller auszumultiplizieren. Ohne Kenntnis der BF müsste man die Klammern auf herkömmlich Art ("jeder mit jedem") ausmultiplizieren.
Beispiel 1
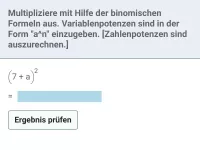
Multipliziere.
a
+
1
2
=
?
3
−
b
2
=
?
11
+
c
·
11
−
c
=
?
Lösung:
- - - - - - - - - - - - - - - - - - - - - -1. BF:
a
+
1
2
=
a
2
+
2
·
a
·
1
+
1
2
=
a
2
+
2a
+
1
- - - - - - - - - - - - - - - - - - - - - -2. BF:
3
−
b
2
=
3
2
−
2
·
3
·
b
+
b
2
=
9
−
6b
+
b
2
- - - - - - - - - - - - - - - - - - - - - -3. BF:
11
+
c
·
11
−
c
=
11
2
−
c
2
=
121
−
c
2
Das Video behandelt weitere Aufgaben:
BINOMISCHE FORMELN – einfach erklärt mit Beispielen
Lernvideo

BINOMISCHE FORMELN – einfach erklärt mit Beispielen

Kanal: MathemaTrick
Beispiel 2
Multipliziere.
3
7
+
y
2
=
?
1,5x
−
2
3
2
=
?
q
2
+
1
6
·
q
2
−
1
6
=
?
Lösung:
- - - - - - - - - - - - - - - - - - - - - -1. BF:
3
7
+
y
2
=
3
7
2
+
2
·
3
7
·
y
+
y
2
=
9
49
+
6
7
 
y
+
y
2
- - - - - - - - - - - - - - - - - - - - - -2. BF:
1,5x
a
−
2
3
b
2
=
1,5x
2
a
2
−
2
·
1,5x
·
2
3
2ab
+
2
3
2
b
2
=
2,25x
2
−
3x
·
2
3
+
4
9
=
2,25x
2
−
2x
+
4
9
- - - - - - - - - - - - - - - - - - - - - -3. BF:
q
2
+
1
6
·
q
2
−
1
6
=
q
2
2
−
1
6
2
=
q
2
4
−
1
36
Das Video behandelt ähnliche Aufgaben.
BINOMISCHE FORMELN mit BRÜCHEN einfach erklärt – viele Beispielen
Lernvideo

BINOMISCHE FORMELN mit BRÜCHEN einfach erklärt – viele Beispielen

Kanal: MathemaTrick
Beispiel 3
Multipliziere.
6
 
x
+
2
 
y
2
=
?
a
3
−
3
 
b
2
=
?
d
+
2
 
3
·
d
−
2
 
3
=
?
- - - - - - - - - - - - - - - - - - - - - - 1. BF:
6
 
x
+
2
 
y
2
=
6
 
x
2
6x
2
+
2
·
6
 
x
·
2
 
y
2
 
12
 
xy
+
2
 
y
2
2y
2
=
6x
2
+
2
 
4
·
3
2
 
3
 
xy
+
2y
2
=
6x
2
+
4
 
3
 
xy
+
2y
2
- - - - - - - - - - - - - - - - - - - - - - 2. BF:
a
3
−
3
 
b
2
=
a
3
2
−
2
·
a
3
·
3
 
b
+
3
 
b
2
=
a
2
9
−
2
3
 
3
 
ab
+
3b
2
- - - - - - - - - - - - - - - - - - - - - - 3. BF:
d
+
2
 
3
·
d
−
2
 
3
=
d
2
−
2
 
3
2
=
d
2
−
2
2
·
3
2
=
d
2
−
4
·
3
=
d
2
−
12
Das Video behandelt weitere Beispiele:
BINOMISCHE FORMELN mit WURZELN einfach erklärt
Lernvideo

BINOMISCHE FORMELN mit WURZELN einfach erklärt

Kanal: MathemaTrick
Beispiel 4
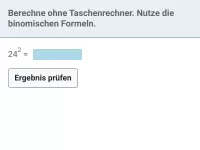
Berechne mithilfe der binomischen Formeln ohne Taschenrechner:
53
2
=
?
29
2
=
?
38
·
42
=
?
Man verwendet hier die 1. binomische Formel und schreibt 53 als die Summe aus 50 und 3. So wird die Einerzahl so klein wie möglich, was das Rechnen im Kopf erleichtert:
53
2
=
50
+
3
2
=
50
2
+
2
·
50
·
3
+
3
2
=
2500
+
300
+
9
=
2809
-----------------------
Man verwendet hier die 2. binomische Formel und schreibt 29 als die Differenz aus 30 und 1. So wird die Einerzahl so klein wie möglich, was das Rechnen im Kopf erleichtert:
29
2
=
30
−
1
2
=
30
2
−
2
·
30
·
1
+
1
2
=
900
−
60
+
1
=
841
-----------------------
Hier nutzt man die 3. binomische Formel und schreibt 38 als die Differenz und 42 als die Summe aus 40 und 2:
38
·
42
=
40
−
2
·
40
+
2
=
40
2
−
2
2
=
1600
−
4
=
1596
Beispiel 5
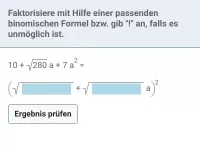
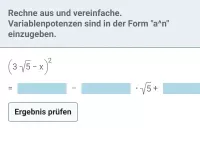
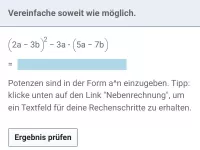
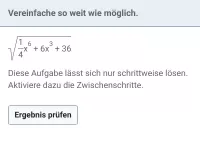
Vereinfache soweit wie möglich.
2c
−
5d
2
−
c
−
5
·
3d
=
?
2c
−
5d
2
−
c
−
5
·
3d
=
2c
2
−
2
·
2c
·
5d
+
5d
2
−
c
·
3d
−
−
5
·
3d
=
4c
2
−
20cd
+
25d
2
−
3cd
+
15d
=
4c
2
−
23cd
+
25d
2
+
15d
Das folgende Video behandelt ein ähnliches Beispiel:
Binomische Formeln anwenden – Terme vereinfachen
Lernvideo

Binomische Formeln anwenden – Terme vereinfachen

Kanal: MathemaTrick
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen