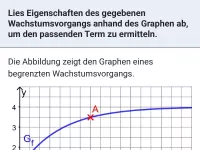
Was ist begrenztes Wachstum und welcher Funktionsterm wird zur Modellierung verwendet?
Wenn der Bestand bei einem Wachstumsvorgang einen bestimmten Wert (die so genannte Schranke S) nicht überschreitet (bzw. bei abnehmendem Bestand nicht unterschreitet), so liegt begrenztes Wachstum vor.
Soll ein begrenzter Wachstumsvorgang durch eine Funktion f beschrieben werden, so wird ein Term der Form \(\displaystyle f(t)=S±c \cdot e^{-kt}\) verwendet. Sein Grenzwert für t gegen ∞ ist S.
Beispiel 1
Die in ℝ definierte Funktion f mit
beschreibt für
einen begrenzten Wachstumsvorgang in Abhängigkeit der Zeit. Ermittle anhand des Funktionsterms …
| = |
|
| 0 |
… die Schranke:
▇
… den Anfangsbestand:
▇
… die Wachstumsgeschwindigkeit nach einer Zeiteinheit:
▇
Der Term
ist stets positiv, nähert sich aber für große Werte von t dem Grenzwert 0 an. Die Schranke des hier vorliegenden Wachstumsvorgangs ist somit 100.
20e |
|
Zum Zeitpunkt
ergibt sich als Anfangsbestand
t | = | 0 |
| = |
|
Die Wachstumsgeschwindigkeit entspricht der Ableitung:
| = |
|
Die Wachstumsgeschwindigkeit für
beträgt somit
t | = | 1 |
| = |
|

Lernvideo
Beschränktes Wachstum verstehen & anwenden – Beispiel mit e-Funktion TEXTAUFGABE
Kanal: Einfach Mathe!
Beispiel 2
Der Marktanteil eines neuen Smartphone-Modells liegt zum Zeitpunkt der Einführung bei 0% und nach einem halben Jahr schon bei 10%. Im weiteren Verlauf nähert sich der Marktanteil sogar einem maximalen Wert von 12% an.
Mit geeigneten Werten für S, c und k soll die zeitliche Entwicklung des Marktanteils durch eine Funktion M beschrieben werden, die jeder Zeit t in Monaten seit der Einführung des neuen Smartphone-Modells den aktuelle Marktanteil
in Prozent zuordnet.
| = |
|
Bestimme zudem, wie schnell der Marktanteil unmittelbar nach Einführung ansteigt.
Der Beschreibung können die Schranke
und das Wertepaar
entnommen werden. Einsetzen in den allgemeinen Term
ergibt:
S | = | 12 |
|
| = |
|
| = |
| Vereinfachen | |||||||||||||||
| = |
|
| |||||||||||||||
c | = | 12 |
Durch Einsetzen des zweiten gegebenen Wertepaars
erhält man:
|
| = |
|
| ||||||||||||||||||||
| = |
|
| ||||||||||||||||||||
| = |
|
| ||||||||||||||||||||
| = |
|
| ||||||||||||||||||||
| = |
| |||||||||||||||||||||
| 0,299 |
Somit lautet ein passender Term:
|
Die Wachstumsgeschwindigkeit entspricht der Ableitung:
| = |
|
Einsetzen von
liefert:
t | = | 0 |
| = |
|
Zum Zeitpunkt der Markteinführung nimmt der Marktanteil des neuen Smartphone-Modells also um 3,6% pro Monat zu.
Siehe auch