Wie berechnet man die Anzahl der Pfade in einem Baumdiagramm mit dem Zählprinzip?

Laut dem Zählprinzip kann man die gesamte Anzahl der Pfade in einem Baumdiagramm berechnen, indem man die Anzahlen der Verzweigungen aller Stufen miteinander multipliziert.

Das funktioniert natürlich nur, wenn innerhalb einer Stufe nicht unterschiedliche Verzweigungszahlen vorliegen.

Beispiel 1

Roman stellt sich ein Menü aus Vor- Haupt- und Nachspeise zusammen. Bei der Vorspeise hat er die Auswahl zwischen X und Y. Bei der Hauptspeise kann er zwischen drei Gerichten A, B und C wählen. Und bei der Nachspeise stehen zwei Optionen R und S zur Auswahl. Wieviele Möglichkeiten hat Roman insgesamt?

Insgesamt

Möglichkeiten.

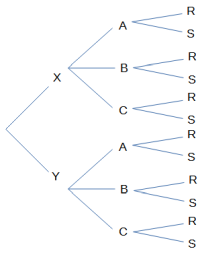
Erklärung am Baumdiagramm: auf der ersten Stufe (Vorspeise) hat man zwei Verzweigungen. Auf der zweiten Stufe (Hauptspeise) liegen jeweils drei Verzweigungen vor. Und auf der letzten Stufe sind es wieder pro Knoten zwei Verzweigungen.

Das Zählprinzip würde nicht funktionieren, wenn man z.B. Vorspeise Y nicht mit Hauptgericht C kombinieren dürfte. Dann nämlich hätte man auf der zweiten Stufe beim oberen Knoten "X" drei Verzweigungen, beim unteren Knoten "Y" dagegen nur zwei.

Beispiel 2

Ein gemischter Chor besteht aus 12 Damen und 8 Herren. Für ein bestimmtes Stück werden zwei Personen benötigt, die dieses im Duett singen. Wie viele Möglichkeiten der Zusammenstellung gibt es theoretisch, wenn

a) das Duett aus einem Mann und einer Frau bestehen soll?

b) das Duett auch aus zwei Männern oder zwei Frauen bestehen kann?

Lösung zu a)

Hier kann man sich ein Baumdiagramm mit zwei Stufen vorstellen:

Erste Stufe: ausgewählter Mann (8 Äste)
Zweite Stufe: ausgewählte Frau (je 12 Äste)

Somit ergeben sich

Kombinationsmöglichkeiten

Lösung zu b)

Hier kann man sich ebenfalls ein Baumdiagramm mit zwei Stufen vorstellen:

Erste Stufe: erste ausgewählte Person (20 Äste)
Zweite Stufe: zweite ausgewählte Person (je 19 Äste)

Somit ergeben sich

380

Kombinationsmöglichkeiten. Doch Vorsicht: dabei kommt jedes Paar zweimal vor, z.B. "Lukas-Toni" und "Toni-Lukas". Da es keine Rolle spielt, wer als erster und wer als zweiter ausgewählt wird, muss man diese Zahl also noch durch 2 teilen und damit sind es 190 mögliche Paare.

Beispiel 3

Wie viele vierstelle natürliche gerade Zahlen kannst du bilden?

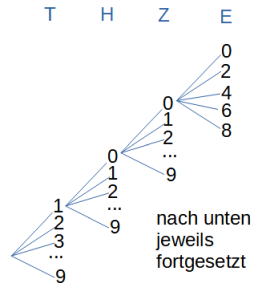
Stelle dir folgendes vierstelliges Baumdiagramm dazu vor:

erste Stufe: Tausenderziffer; möglich sind die Ziffern 1-9 (0 nicht, sonst wäre die Zahl nicht vierstellig); also 9 Äste
zweite Stufe: Hunderterziffer; möglich sind 0-9; also je 10 Äste
dritte Stufe: Zehnerziffer; möglich sind 0-9; also je 10 Äste
vierte Stufe: Einerziffer; möglich sind 0, 2, 4, 6 und 8 (Zahl soll gerade sein); also je 5 Äste

Laut Zählprinzip gibt es also