Wie sind Sinus und Kosinus am Einheitskreis definiert?
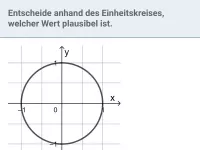
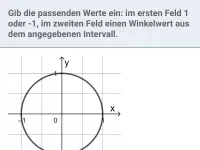
Jedem Winkel α lässt sich auf dem Einheitskreis genau ein Punkt P(x|y) zuordnen. Der Winkel wird dabei von der positiven x-Achse aus entgegen dem Uhrzeigersinn gedreht. Man definiert:
cos(α) = x und sin(α) = y
Sinus- und Kosinuswerte können also als Koordinaten von Punkten des Einheitskreises aufgefasst werden.Beispiel 1
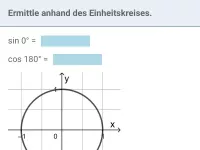
Ermittle anhand des Einheitskreises:
| = | ? |
| = | ? |
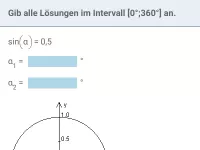
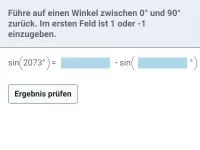
Vorgehen: Ziehe alle Vielfachen von 360° vom Argument (Wert in der Klammer) ab und beantworte dann anhand des Einheitskreises.
| = |
| ||||||||||||||||||
|
| = |
| ||||||||||||||||||
|
| = |
| ||||||||||||||||||
| = |
| ||||||||||||||||||
|
| = |
| ||||||||||||||||||
|
| = |
| ||||||||||||||||||

Lernvideo
Trigonometrie, Sinus und Kosinus am Einheitskreis, Beispiel 1
Kanal: Mathegym
Beispiel 2
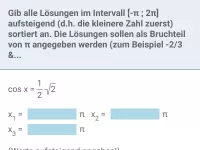
Mit welchen der folgenden vier Werte stimmt
überein? Entscheide anhand des Einheitskreises.
cos |
|
|
|
cos |
|
|
|
cos |
|
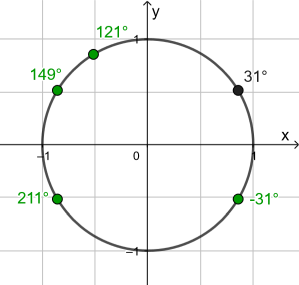
Vergleiche die grünen Punkte mit dem schwarzen hinsichtlich der x-Koordinate (=Kosinuswert). Bei −31° liegt derselbe (positive) Kosinuswert vor, bei 149° und 211° ist der Kosinuswert vom Betrag her gleich, aber vom Vorzeichen her negativ. Der Winkel 121° weicht demgegenüber vom Betrag her ab. Also gilt:
cos |
|
≠ |
|
≠ |
|
= |
|
≠ |
|

Lernvideo
Trigonometrie, Sinus und Kosinus am Einheitskreis, Beispiel 3
Kanal: Mathegym
Siehe auch