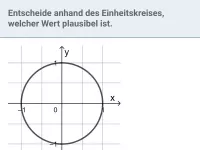
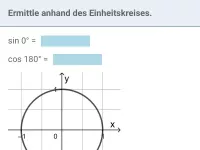
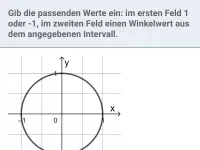
Wie beeinflusst die Spiegelung eines Punktes P auf dem Einheitskreis an der x-Achse, y-Achse oder am Ursprung die Sinus- und Kosinuswerte?
Sei P der Punkt des Einheitskreises, der dem Winkel α zugeordnet ist.
| Winkel | Spiegelung von P | Vorzeichenänderung | Formeln |
| −α bzw. 360° − α |
an der x-Achse | nur sin | sin(α) = − sin(360° − α) cos(α) = cos(360° − α) |
| 180° − α | an der y-Achse | nur cos | sin(α) = sin(180° − α) cos(α) = − cos(180° − α) |
| α ± 180° | am Ursprung | sin und cos | sin(α) = − sin(α ± 180°) cos(α) = − cos(α ± 180°) |
| α ± 360° | P verändert sich nicht | sin(α) = sin(α ± 360°) cos(α) = cos(α ± 360°) |
|
Beispiel 1
Führe sin(139°) auf einen Winkel im Intervall [180° ; 270°] zurück.
Spiegelung an der x-Achse, um einen Winkel im geforderten Intervall zu erhalten:
| = | 221° |
Da sich bei der Spiegelung an der x-Achse der Sinuswert vom Vorzeichen her umdreht, muss −1 vor den neuen Sinuswert geschrieben werden:
sin(139°) | = |
|

Lernvideo
Trigonometrie, Sinus und Kosinus am Einheitskreis, Beispiel 2
Kanal: Mathegym
Beispiel 2
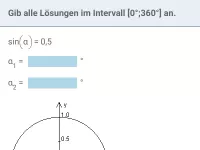
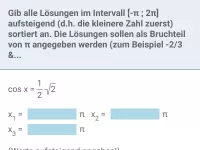
Gib alle Lösungen im Intervall [0°;360°] an.
| = | 0,7 |
sin(x)
y | = | 0,7 |
| = | 0,7 |
β | = |
|
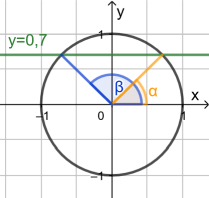
Laut Taschenrechner gilt
[achte darauf, dass der TR auf Gradmaß ("Degree") eingestellt ist]. Dieser Wert entspricht dem oben abgebildeten Winkel α. Der zweite abgebildete Winkel ergibt sich dann durch
| 44,4° |
| = | 135,6°. |
Damit lauten die Lösungen
und
|
|
|
|

Lernvideo
Trigonometrie, Beispiel Gleichung
Kanal: Mathegym
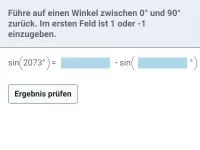
Beispiel 3
Führe cos(2314°) auf einen Winkel zwischen 0° und 90° zurück:
Lösung:
Ziehe zunächst das größtmögliche Vielfache von 360° raus:
| = | 6 Rest 154 |
cos(2314°) | = | cos(154°) |
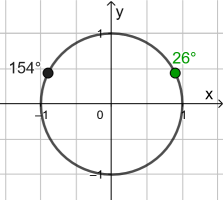
Um auf einen Winkel im geforderten Intervall zu kommen, muss man 154° an der y-Achse spiegeln:
| = | 26° |
Da sich bei der Spiegelung an der y-Achse der Kosinuswert vom Vorzeichen her ändert, muss vor den neuen Kosinuswert noch ein Minuszeichen gesetzt werden:
cos(2314°) | = |
|
Siehe auch