Wie sehen die Diagramme bei proportionalen und umgekehrt proportionalen Beziehungen aus?

Jede Wertetabelle lässt sich grafisch umsetzen, indem man die einzelnen Spalten als Punkte mit entsprechender x- und y-Koordinate liest.

Merke:

Bei Proportionalität ergibt sich eine Gerade, die durch den Ursprung des Koordinatensystems geht.
Bei umgekehrter Proportionalität (Antiproportionalität) ergibt sich eine sogenannte Hyperbel, deren Äste sich auf die x- und y-Achse zubewegen.

Beispiel

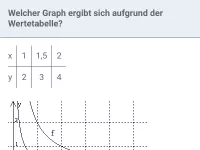
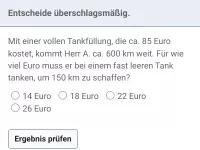
Welcher Graph beschreibt den Zusammenhang zwischen der Fahrzeit und der durchschnittlichen Geschwindigkeit bei einer Strecke von 400 km?

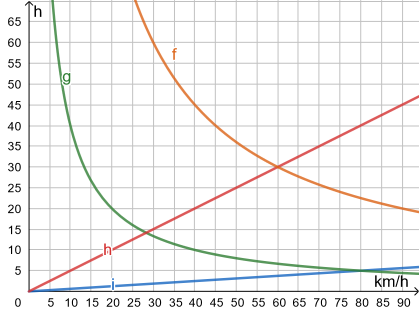
Die Größen "Zeit" und "Geschwindigkeit" sind umgekehrt proportional (antiproportional), daher scheiden die Geraden h und i aus. [Erläuterung: Geraden geben den Zusammenhang proportionaler Größen wieder.]

Bleiben noch f und g übrig. Auf dem Graphen von g lesen wir z.B. den Punkt (80|5) ab. Überprüfen wir also, ob bei einer Strecke von 400 km und einer Gechwindigkeit von 80 km/h die Fahrzeit 5 h beträgt:

5 h

400 km

Ja, die Werte passen zusammen, also ist Graph g die richtige Antwort.

--- Zweiter Lösungsweg ---

Man geht von einem beliebigen Wert der km/h-Skala aus, z.B. 50, berechnet den zugehörigen km-Wert und überpüft dann, auf welchem Graphen der Punkt liegt:

Bei 50 km/h bräuchte man für 50 km 1 h und für 400 km folglich 8 h. Der Punkt (50|8) liegt auf dem Graphen g.