Welche typischen Eigenschaften und Merkmale hat die quadratische Funktion y=x² und ihr Graph?
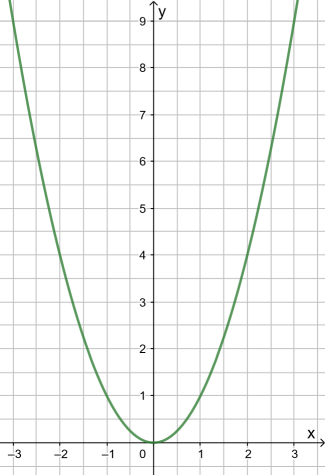
Der Graph der quadratischen Funktion y=x² heißt Normalparabel mit dem Scheitel S ( 0 | 0 ).
Eigenschaften der Funktion / des Graphen:
- Die Funktion y=x² ordnet jedem x-Wert seine Quadratzahl x² zu.
- Damit gilt: der y-Wert einer Zahl x und der y-Wert ihrer Gegenzahl -x sind immer gleich. Deshalb ist der Graph achsensymmetrisch zur y-Achse.
- Der kleinste Funktionswert ist 0. Alle anderen Funktionswerte sind positiv.
- Der tiefste Punkt des Graphen heißt Scheitel. Er liegt bei der Normalparabel im Ursprung.
Beispiel 1
Bestimme den zugehörigen y-Wert zum gegebenen x-Wert:
y | = |
|
x | = |
|
y | = | ▇ |
| = |
|
| = |
|
| |||||||||
| = |
| Potenz berechnen | |||||||||
| = |
| ||||||||||
Hinweis: Die Klammer ist beim Potenzieren von negativen Zahlen wichtig und darf nicht weggelassen werden, besonders dann nicht, wenn du den Taschenrechner verwendest. Wenn du die Klammer nicht miteingibst, erhältst du ein falsches negatives Ergebnis!
Beispiel 2
Überprüfe, ob der gegebene Punkt auf der Normalparabel mit dem Scheitel S (0 | 0) liegt.
Normalparabel y | = |
|
P (12 | 120)
P (12 | 120):
| = | 144 und nicht 120. |
Zur x-Koordinate 12 ist 144 die passende y-Koordinate.
Also liegt der Punkt (12 | 144) auf der Normalparabel mit dem Scheitel S (0 | 0) und nicht P (12 | 120).
(Für Experten: Da 120 < 144, liegt P unterhalb der Normalparabel.)
Beispiel 3
Bestimme, falls möglich, alle x-Werte, für die die Punkte P und Q auf der Normalparabel mit dem Scheitel S ( 0 | 0 ) liegen.
Normalparabel y | = |
|
Punkt P ( x | )
64
Punkt Q ( x |
)
− | 64 |
Punkt P ( x | )
64
Es gilt:
| = |
|
| ||||||||||
| = |
| Wurzel ziehen | ||||||||||
| = |
| ausrechnen | ||||||||||
| = |
| |||||||||||
| = |
| |||||||||||
Hinweis: Denke daran, dass es beim Wurzelziehen oft zwei Lösungen - eine positive und eine negative - gibt.
Punkt Q ( x |
)
− | 64 |
Es gilt:
| = |
|
| |||||||||
| = |
| Wurzel ziehen | |||||||||
| = |
| Das geht nicht! Aus einer negativen Zahl kannst du keine Wurzel ziehen. | |||||||||
Der Punkt Q liegt nicht auf der Normalparabel mit dem Scheitel S ( 0 | 0 ).