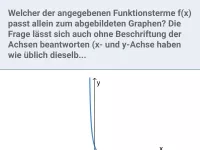
Wie erkennt man bei gebrochen-rationalen Funktionen die Asymptoten des Graphen?
Liegt eine gebrochen-rationale Funktion in der Form p(x)/q(x) vor, so kann man anhand des Zählergrads z (also die höchste x-Potenz im Zähler) und des Nennergrads n erkennen, ob der Graph eine waagrechte oder schräge Asymptote besitzt.
- x-Achse als waagrechte Asymptote, falls z < n
- waagrechte Asymptote, aber nicht die x-Achse, falls z = n; es genügt, die Leitkoeffizienten abzulesen und zu dividieren
- schräge Asymptote, falls z = n + 1; die Gleichung lässt sich durch Polynomdivision ermitteln
- weder waagrechte noch schräge Asymptote, falls z > n + 1
Beispiel
Liegen waagrechte/schräge Asymptoten vor? Wenn ja, bestimme deren Gleichung.
| = |
|
| = |
|
| = |
|
| = |
|
Lösung:
| = |
|
Es liegt eine waagrechte Asymptote ungleich der x-Achse vor, da Zählergrad = Nennergrad. Die Gleichung ergibt sich aus dem Quotienten der Leitkoeffizienten:
|
| = |
|
Zählergrad > Nennergrad + 1, daher liegt keine schräge Asymptote (erst recht keine waagrechte) vor.
| = |
|
Zählergrad < Nennergrad, daher ist die x-Achse waagrechte Asymptote.
| = |
|
Zählergrad = Nennergrad + 1, daher liegt eine schräge Asymptote vor. Deren Bestimmung erfordert in diesem Fall die Polynomdivision als Technik (genauer im Video erklärt). Je nach Bundesland und Schulart geht dies über den Lehrplan hinaus.

Lernvideo
Gebrochen-rationale Funktionen, Asymptotenbestimmung, Beispiel
Kanal: Mathegym
Siehe auch