Gebrochen-rationale Funktionen, Mathe-Aufgaben
Gebrochen-rationale Funktionen, Aufgaben und Online-Übungen inkl. Lösung, Erklär-Videos und Hilfestellungen.
Auf unserer mehrfach prämierten Mathe-Lernplattform, die auch an 588 Schulen verwendet wird.
Viele unterschiedliche Mathe-Aufgaben und Mathe-Übungen zu 291 Themen der Schulmathematik.

-
≈8. Klasse - Aufgaben + Stoff + Video
Elementare gebrochen-rationale Funktionen
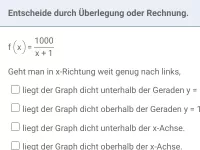
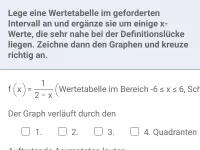
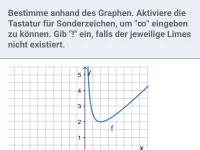
Definitionslücken und Verhalten der Funktion in deren Umgebung, Erkennen waagrechter und senkrechter Asymptoten, Grafen ohne Wertetabelle skizzieren -
≈Oberstufe - Aufgaben + Stoff + Video
Funktionsuntersuchung - gebrochen-rationale Funktionen
Symmetrie zum KOSY, Nullstellen, Monotonie, Hoch- und Tiefpunkte -
≈Oberstufe - Aufgaben + Stoff
Gebrochen-rationale Funktionen - Definitionsmenge und Nullstellen
Bestimmung der maximalen Definitionsmenge und der Nullstelle(n) -
≈Oberstufe - Aufgaben + Stoff + Video
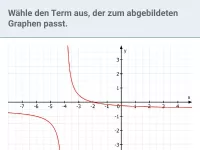
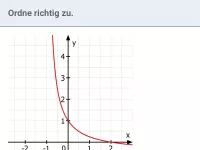
Gebrochen-rationale Funktionen - Funktionsterm und Graph
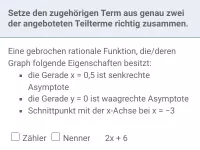
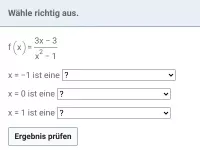
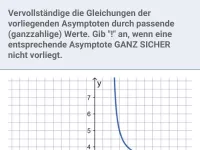
Gebrochen-rationale Funktionen hinsichtlich Definitionsmenge, Polstellen, Nullstellen, Asymptoten untersuchen und den Graph zeichnen; den Term einer gebrochen-rationalen Funktion anhand gegebener Eigenschaften bestimmen -
≈Oberstufe - Aufgaben + Stoff
Gebrochen-rationale Funktionen - gemischte Aufgaben
Gemischte Aufgaben zum Thema gebrochen-rationale Funktionen -
≈Oberstufe - Aufgaben + Stoff + Video
Gebrochen-rationale Funktionen - Polstellen
Verhalten von f(x) in der Umgebung von Definitionslücken -
≈Oberstufe - Aufgaben + Stoff
Gebrochen-rationale Funktionen - Schnittpunkte von Graphen
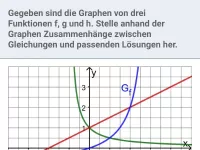
Schnittpunkte zwischen den Graphen gebrochen-rationaler Funktionen und linearer Funktionen rechnerisch bestimmen. Zu einem Diagramm mit sich schneidenden Graphen zugehörige Gleichungen bestimmen und die Anzahl der Lösungen angeben. -
≈Oberstufe - Aufgaben + Stoff + Video
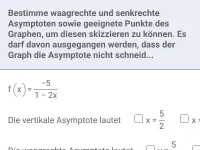
Gebrochen-rationale Funktionen - waagrechte und schräge Asymptoten
Verhalten von f(x) für x→±∞; Bestimmung der Gleichung von waagrechten und schrägen Asymptoten
Fragen und Antworten zum Thema "gebrochen-rationale Funktionen"
- Was muss bei der Definitionsmenge gebrochen-rationaler Funktionen beachtet werden?
- Wie lautet die korrekte Schreibweise für eine Definitionsmenge, die alle rationalen Zahlen außer bestimmten Werten enthält?
- Was versteht man unter Asymptoten und wie werden sie dargestellt?
- Wie sind die Quadranten 1 bis 4 im Koordinatensystem angeordnet?
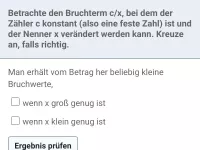
- Wie verändert sich der Wert eines Bruchs bei Veränderung des Nenners bei konstantem Zähler?
- Was sind die Erkennungsmerkmale von gebrochen-rationalen Funktionen?
- Warum reichen Asymptoten einer gebrochen-rationalen Funktion nicht aus, um den Grafen genau zu skizzieren?
- Was sind Polstellen bei gebrochen-rationalen Funktionen und wie verhält sich der Graph in ihrer Umgebung?
- Wie bestimmt und spezifiziert man eine Polstelle in der Mathematik?
- Was versteht man unter einer behebbaren Definitionslücke?
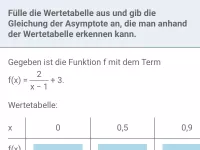
- Wie erkennt man bei gebrochen-rationalen Funktionen die Asymptoten des Graphen?
- Was sind die wesentlichen Aspekte einer vollständigen Funktionsuntersuchung?
- Was bedeutet der Limes von f(x) für x → c− bzw. x → c+?
- Was passiert mit einem Bruch, wenn der Zähler konstant ≠ 0 ist und der Nenner gegen 0 strebt?
- Wie bestimmt man das Verhalten einer gebrochen-rationalen Funktion für x gegen Unendlich?
- Wie lassen sich Bruchterme vereinfachen und welche Techniken sind dabei hilfreich?
- Wie erkennt man Achsen- und Punktsymmetrie bei Funktionen, insbesondere bei ganzrationalen Funktionen?
- Wie beeinflussen die Parameter b und c den Graphen einer gebrochen-rationalen Funktion y=a/(x+b)+c?
- Wie beeinflusst der Parameter a den Graphen der Funktion y=a/x?
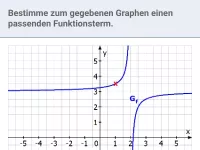
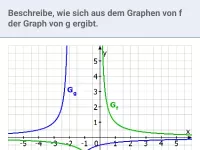
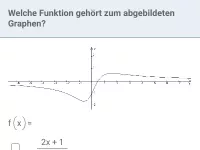
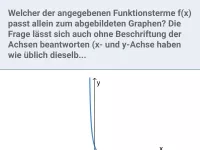
- Wie leitet man den Funktionsterm einer gebrochen-rationalen Funktion aus ihrem Graphen ab?
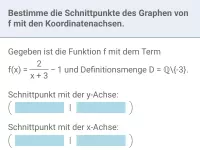
- Wie bestimmt man die Schnittpunkte eines Graphen einer gebrochen-rationalen Funktion mit den Koordinatenachsen?
- Wie löst man eine Bruchgleichung, wenn x nur im Nenner eines Bruchs vorkommt?
- Wie bestimmt man die Definitionsmenge und Nullstellen bei gebrochen-rationalen Funktionen?
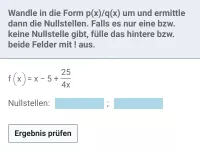
- Wie kann man eine gebrochen-rationale Funktion der Form a(x)+b(x)/c(x) in die Form p(x)/q(x) umwandeln?
- Wie bestimmt man die x-Koordinaten der Schnittpunkte zweier Graphen?