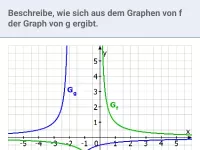
Was versteht man unter Asymptoten und wie werden sie dargestellt?
Asymptoten sind Geraden, denen sich der Graph annähert. Der Graph kommt der Asymptote dabei beliebig nahe, ohne sie zu berühren.
Oftmals sind Asymptoten senkrecht oder waagrecht verlaufende Geraden. Z.B.:
- "y = 5" drückt eine waagrechte Gerade durch den Punkt (0|5) aus.
- "x = 5" drückt eine senkrechte Gerade durch den Punkt (5|0) aus.
Beispiel 1
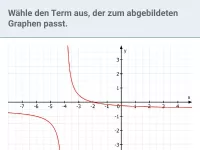
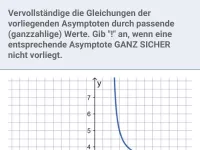
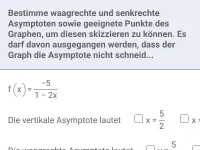
Bestimme alle waagrechten und senkrechten Asymptoten des Graphen und gib ihre Gleichungen an.

Lösung:
- waagrechte Asymptote
Wie verhält sich der Graph für sehr große bzw. sehr kleine x-Werte (also an den "Rändern")? Offensichtlich schmiegt er sich an die waagrechte Gerade mit der Gleichung
an. Er kommt dieser Geraden beliebig nahe, wenn man nur weit genug nach rechts oder links geht.
|
- senkrechte Asymptote
Wie man sieht, schmiegt sich der Graph auch der y-Achse an, genauer: Für x-Werte nahe 0 werden die zugehörigen y-Werte beliebig groß bzw. beliebig klein. Die y-Achse mit der Gleichung
ist also eine senkrechte Asymptote des Graphen.
|

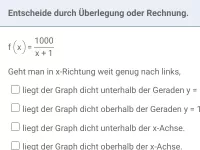
Beispiel 2
Gegeben ist die Funktion f mit dem Term
f(x) | = |
|
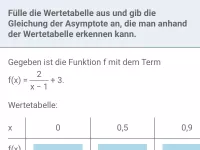
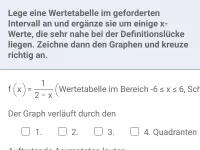
Fülle die Lücken in der Wertetabelle aus und gib die Gleichung der Asymptote an, die man daraus erkennen kann.
|
|
|
|
|
| |||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||
|
|
|
|
|
|
Wenn man x-Werte einsetzt, die dem Wert
immer näherkommen, wächst der Betrag der zugehörigen y-Werte stark an. Der Graph von f nähert sich also der senkrechten Asymptote mit der Gleichung
an.
x | = |
|
|
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈8. Klasse - Aufgaben + Stoff + Video
Elementare gebrochen-rationale Funktionen
Definitionslücken und Verhalten der Funktion in deren Umgebung, Erkennen waagrechter und senkrechter Asymptoten, Grafen ohne Wertetabelle skizzieren -
≈Oberstufe - Aufgaben + Stoff
Gebrochen-rationale Funktionen - gemischte Aufgaben
Gemischte Aufgaben zum Thema gebrochen-rationale Funktionen
Ähnliche Themen
- Was muss bei der Definitionsmenge gebrochen-rationaler Funktionen beachtet werden?
- Wie lautet die korrekte Schreibweise für eine Definitionsmenge, die alle rationalen Zahlen außer bestimmten Werten enthält?
- Wie sind die Quadranten 1 bis 4 im Koordinatensystem angeordnet?
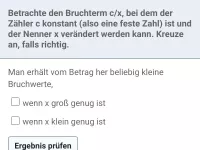
- Wie verändert sich der Wert eines Bruchs bei Veränderung des Nenners bei konstantem Zähler?
- Was sind die Erkennungsmerkmale von gebrochen-rationalen Funktionen?
- Warum reichen Asymptoten einer gebrochen-rationalen Funktion nicht aus, um den Grafen genau zu skizzieren?
- Wie beeinflussen die Parameter b und c den Graphen einer gebrochen-rationalen Funktion y=a/(x+b)+c?
- Wie beeinflusst der Parameter a den Graphen der Funktion y=a/x?
- Wie leitet man den Funktionsterm einer gebrochen-rationalen Funktion aus ihrem Graphen ab?
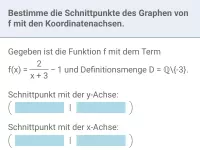
- Wie bestimmt man die Schnittpunkte eines Graphen einer gebrochen-rationalen Funktion mit den Koordinatenachsen?