Wie bestimmt man die Schnittpunkte eines Graphen einer gebrochen-rationalen Funktion mit den Koordinatenachsen?
Der Graph einer gebrochen-rationalen Funktion kann die x-Achse und die y-Achse schneiden.
Punkte auf der x-Achse haben y-Koordinate 0, Punkte auf der y-Achse haben x-Koordinate 0.
Vorgehensweise, um die jeweils fehlende Koordinate zu bestimmen:
- Schnittpunkt mit der x-Achse: Löse die Gleichung f(x) = 0.
- Schnittpunkt mit der y-Achse: Berechne f(0).
Beispiel 1
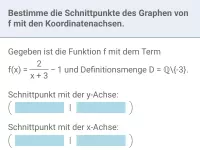
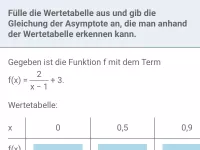
Gegeben ist die Funktion f mit dem Term
und Definitionsmenge D = ℝ\{2}. Bestimme die Schnittpunkte des Graphen von f mit den Koordinatenachsen.
f(x) | = |
|
Lösung:
- Schnittpunkt mit der y-Achse:
Punkte auf der y-Achse besitzen x-Koordinate 0, also:
| = | 1 |
Schnittpunkt:
|
- Schnittpunkt mit der x-Achse:
Punkte auf der x-Achse besitzen y-Koordinate 0, also:
| = |
|
| ||||||||||||||
| = |
| Der Nenner muss den Wert 2 haben | ||||||||||||||
| = |
|
| ||||||||||||||
| = |
| |||||||||||||||
Schnittpunkt:
|
Beispiel 2
Gegeben ist die Funktion f mit dem Term
und Definitionsmenge D = ℝ\{2}. Bestimme die Schnittpunkte des Graphen von f mit den Koordinatenachsen.
f(x) | = |
|
Lösung:
Punkte auf der y-Achse besitzen x-Koordinate 0, also:
| = | 1 |
Schnittpunkt:
|
Punkte auf der x-Achse besitzen y-Koordinate 0, also:
| = |
|
| |||||||||||||||||||
| = |
|
| |||||||||||||||||||
| = |
| Ausmultiplizieren | |||||||||||||||||||
| = |
|
| |||||||||||||||||||
| = |
|
| |||||||||||||||||||
| = |
| ||||||||||||||||||||
Schnittpunkt:
|
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈8. Klasse - Aufgaben + Stoff + Video
Bruchgleichungen
Lösung mittels Graf, kreuzweiser Multiplikation bzw. Multiplikation mit dem Hauptnenner; Einschränkungen für x und Proberechnung; Textaufgaben; Lösungsformel für quadratische Gleichungen nicht erforderlich -
≈8. Klasse - Aufgaben + Stoff + Video
Elementare gebrochen-rationale Funktionen
Definitionslücken und Verhalten der Funktion in deren Umgebung, Erkennen waagrechter und senkrechter Asymptoten, Grafen ohne Wertetabelle skizzieren -
≈Oberstufe - Aufgaben + Stoff
Gebrochen-rationale Funktionen - Schnittpunkte von Graphen
Schnittpunkte zwischen den Graphen gebrochen-rationaler Funktionen und linearer Funktionen rechnerisch bestimmen. Zu einem Diagramm mit sich schneidenden Graphen zugehörige Gleichungen bestimmen und die Anzahl der Lösungen angeben.
Ähnliche Themen
- Wie lautet die Lösung der Gleichung 1/x = a?
- Warum müssen bei Bruchgleichungen bestimmte Werte für x ausgeschlossen werden?
- Welche Überprüfungen sind nach der Umformung einer Bruchgleichung notwendig?
- Wie macht man eine Bruchgleichung nennerfrei und was sollte man beachten?
- Wie liest man die Lösungen einer Bruchgleichung b<sub>1</sub>(x) = b<sub>2</sub>(x) aus einem Diagramm ab?
- Was muss bei der Definitionsmenge gebrochen-rationaler Funktionen beachtet werden?
- Was versteht man unter Asymptoten und wie werden sie dargestellt?
- Was sind die Erkennungsmerkmale von gebrochen-rationalen Funktionen?
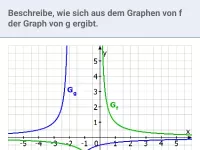
- Wie beeinflussen die Parameter b und c den Graphen einer gebrochen-rationalen Funktion y=a/(x+b)+c?
- Wie beeinflusst der Parameter a den Graphen der Funktion y=a/x?
- Wie leitet man den Funktionsterm einer gebrochen-rationalen Funktion aus ihrem Graphen ab?
- Wie löst man eine Bruchgleichung, wenn x nur im Nenner eines Bruchs vorkommt?
- Wie bestimmt man die x-Koordinaten der Schnittpunkte zweier Graphen?
- Wie löst man Bruchgleichungen der Form a / b = c / d am einfachsten?
- Wie stellt man eine Formel um, sodass eine Variable allein steht?