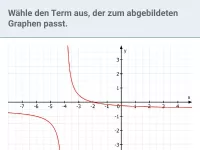
Wie leitet man den Funktionsterm einer gebrochen-rationalen Funktion aus ihrem Graphen ab?
Anhand der Asymptoten und mithilfe eines Punkts des Graphen kann man bei elementaren gebrochen-rationalen Funktionen vom Graphen auf den Funktionsterm schließen (siehe Beispiel).
Beispiel
Für elementare gebrochen-rationale Funktionen kann man aus einem gegebenen Graphen auf den zugehörigen Funktionsterm der Form
schließen, indem man …
f(x) | = |
|
- … die senkrechte und die waagrechte Asymptote am Graphen abliest,
- … damit im Funktionsterm die Werte der Paramter b und c festlegt,
- … einen Punkt des Graphen abliest und die Koordinaten dieses Punkts in den Funktionsterm einsetzt ("Punktprobe")
- … und die entstehende Gleichung nach dem Parameter a auflöst, um auch dessen Wert zu bestimmen.
Den gesuchten Funktionsterm erhält man schließlich durch Einsetzen der Werte von a, b und c in den allgemeinen Funktionsterm.
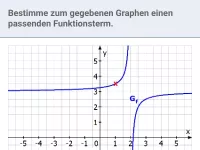
Aufgabenbeispiel:
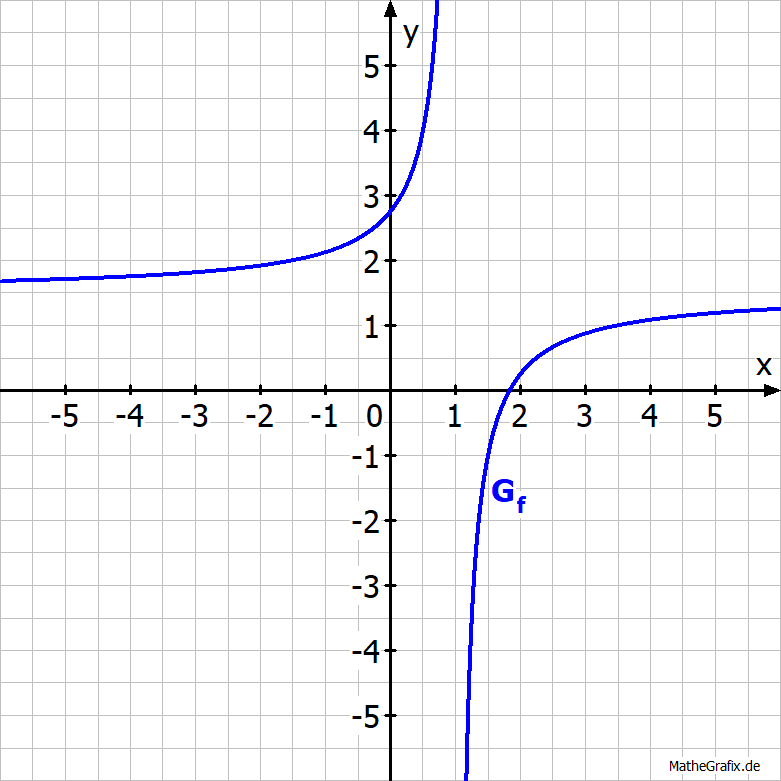
Bestimme den zum Graphen passenden Funktionsterm.
Lösung:
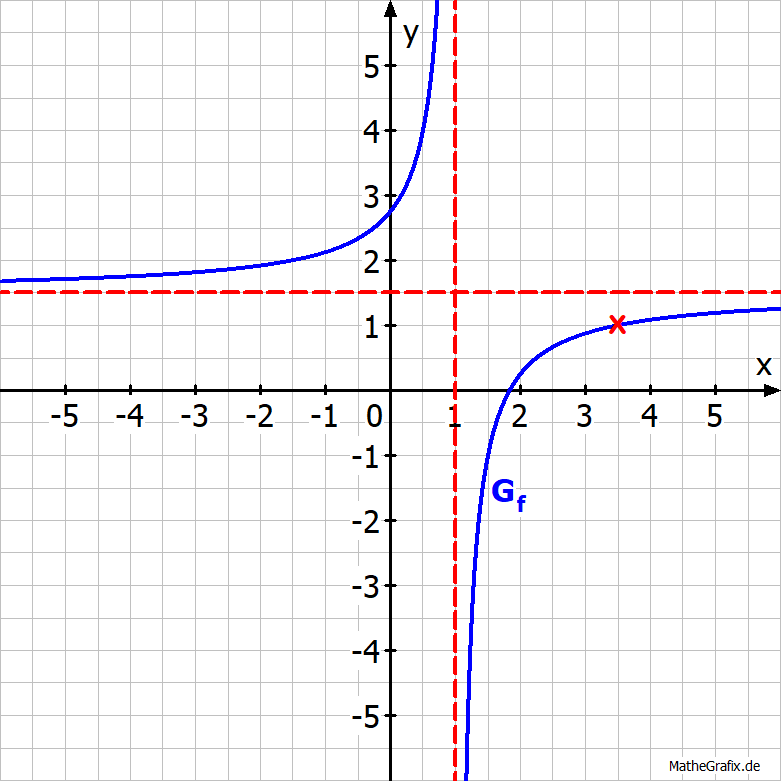
- Ablesen der Asymptoten:
Der Graph besitzt die Asymptoten mit den Gleichungen
und
x | = | 1 |
y | = | 1,5. |
Daraus ergeben sich die Werte
und
und man kann schreiben:
b | = |
|
c | = | 1,5 |
f(x) | = |
|
- Bestimmung von a mithilfe eines Punkts des Graphen:
Der Graph verläuft durch den Punkt
, es gilt also
|
f(3,5) | = | 1. |
Einsetzen ergibt:
| = |
|
| ||||||||||||
| = |
|
| ||||||||||||
Es folgt:
a | = |
|
- Aufstellen des passenden Funktionsterms:
|
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
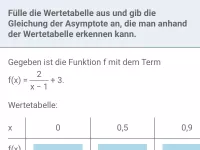
- Was muss bei der Definitionsmenge gebrochen-rationaler Funktionen beachtet werden?
- Was versteht man unter Asymptoten und wie werden sie dargestellt?
- Was sind die Erkennungsmerkmale von gebrochen-rationalen Funktionen?
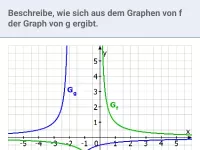
- Wie beeinflussen die Parameter b und c den Graphen einer gebrochen-rationalen Funktion y=a/(x+b)+c?
- Wie beeinflusst der Parameter a den Graphen der Funktion y=a/x?
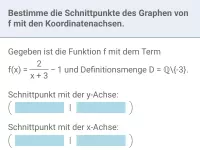
- Wie bestimmt man die Schnittpunkte eines Graphen einer gebrochen-rationalen Funktion mit den Koordinatenachsen?