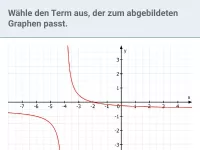
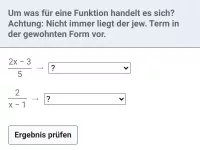
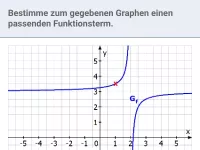
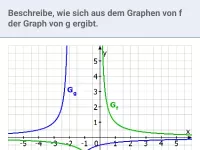
Wie beeinflusst der Parameter a den Graphen der Funktion y=a/x?
Der Parameter a im Term einer gebrochen-rationalen Funktion mit der Gleichung y=a/x kann eine Streckung in y-Richtung und eine Spiegelung an der x-Achse bewirken (siehe Beispiel).
Beispiel
Den Graphen der Funktion g mit dem Term
erhält man aus dem Graphen der Funktion f mit dem Term
durch
g(x) | = |
|
f(x) | = |
|
- Streckung um den Faktor |a| in y-Richtung und,
- falls a negativ ist, durch Spiegelung an der x-Achse.
Aufgabenbeispiel:
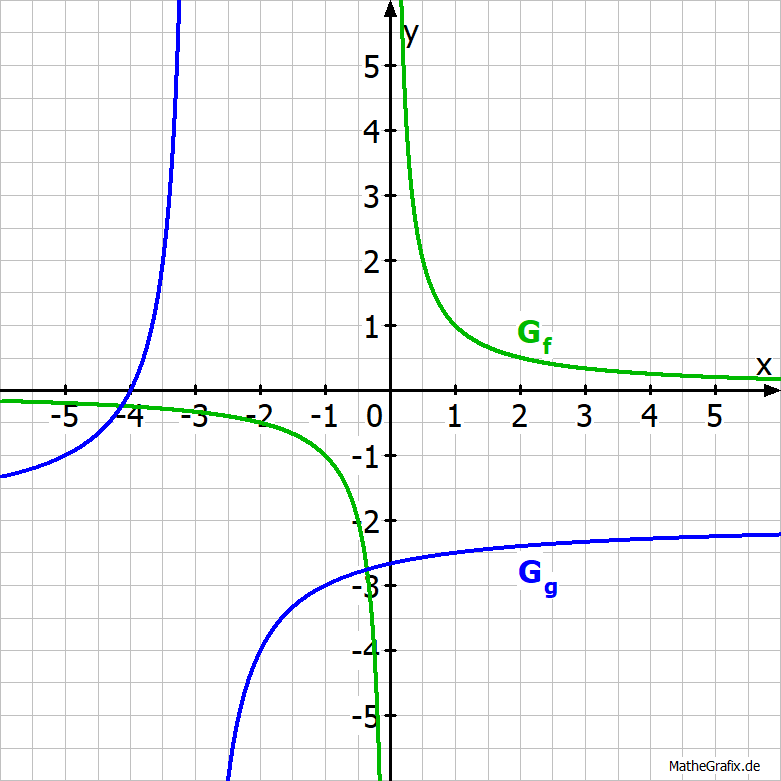
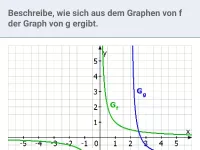
Beschreibe, wie der Graph von g aus dem Graphen von f mit dem Term
hervorgeht, und gib einen passenden Funktionsterm für g an.
f(x) | = |
|
Lösung:
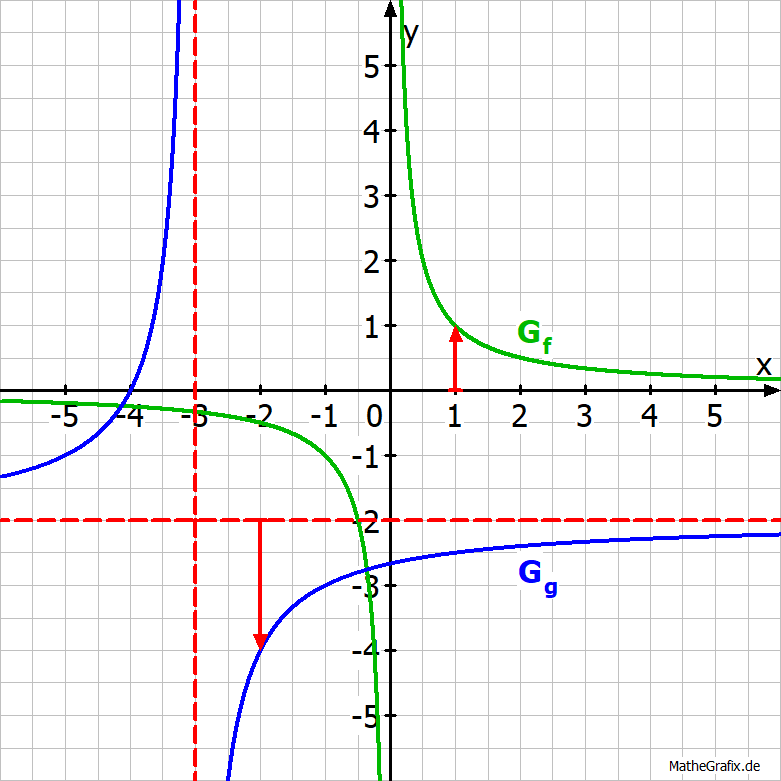
Die roten Pfeile in der Abbildung und die gestrichelt dargestellten Asymptoten zeigen:
Der Graph von g entsteht aus dem Graphen von f durch
- Streckung mit Faktor 2 in y-Richtung und
- Spiegelung an der x-Achse, sowie
- Verschiebung um 3 nach links und
- Verschiebung um 2 nach unten.
Der zugehörige Funktionsterm lautet
g(x) | = |
|
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Was muss bei der Definitionsmenge gebrochen-rationaler Funktionen beachtet werden?
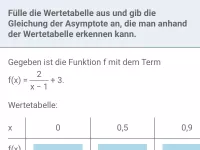
- Was versteht man unter Asymptoten und wie werden sie dargestellt?
- Was sind die Erkennungsmerkmale von gebrochen-rationalen Funktionen?
- Wie beeinflussen die Parameter b und c den Graphen einer gebrochen-rationalen Funktion y=a/(x+b)+c?
- Wie leitet man den Funktionsterm einer gebrochen-rationalen Funktion aus ihrem Graphen ab?
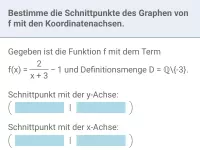
- Wie bestimmt man die Schnittpunkte eines Graphen einer gebrochen-rationalen Funktion mit den Koordinatenachsen?