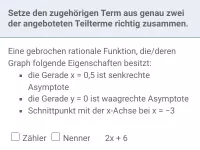
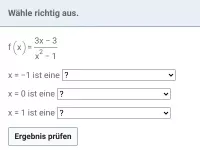
Wie erkennt man Achsen- und Punktsymmetrie bei Funktionen, insbesondere bei ganzrationalen Funktionen?

  • Achsensymmetrie zur y-Achse:
    • Für alle x aus dem Definitionsbereich gilt:
    f(x) = f(-x)

  • Punktsymmetrie zum Ursprung:
    • Für alle x aus dem Definitionsbereich gilt:
    -f(x) = f(-x)

  • Spezialfall: ganzrationale Funktionen

    • f(x) = f(-x) gilt genau dann, wenn nur gerade Exponenten auftauchen.
    Also gilt:
    Hat eine ganzrationale Funktion nur x-Potenzen mit geraden Hochzahlen, so ist der Graph der Funktion achsensymmetrisch zur y-Achse.

    -f(x) = f(-x) gilt genau dann, wenn nur ungerade Exponenten auftauchen.
    Also gilt:
    Hat eine ganzrationale Funktion nur x-Potenzen mit ungeraden Hochzahlen, so ist der Graph der Funktion punktsymmetrisch zum Ursprung.

  • Hinweis:
    • Die einzige Funktion deren Graph sowohl achsensymmetrisch zur y-Achse also auch punktsymmetrisch zum Ursprung ist, ist f(x)=0.
Beispiel 1
Untersuche, ob der Graph der Funktion achsensymmetrisch zur y-Achse oder punktsymmetrisch zum Ursprung ist.
a) 
f
 
x
=
5x
2
x
2
+
2
b) 
f
 
x
=
5x
2
x
3
+
2x
c) 
f
 
x
=
5x
2
x
3
+
2
Zu a)
  • Achsensymmetrie zur y-Achse?
Kriterium:
f
 
x
=
f
 
−
x
f
 
x
=
5x
2
x
2
+
2
f
 
−
x
=
5
·
−
x
2
−
x
2
+
2
=
5x
2
x
2
+
2
=
f(x)
Also gilt:
f
 
−
x
=
f
 
x
Der Graph der Funktion ist achsensymmetrisch zur y-Achse.
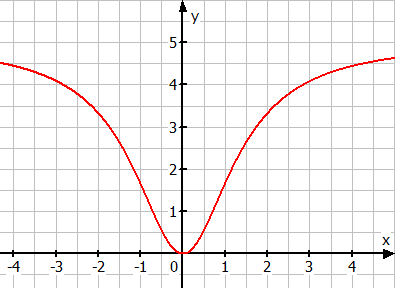
graphik
Zu b)
  • Achsensymmetrie zur y-Achse?
Kriterium:
f
 
x
=
f
 
−
x
f
 
x
=
5x
2
x
3
+
2x
f
 
−
x
=
5
·
−
x
2
−
x
3
+
2
·
−
x
=
5x
2
−
x
3
−
2x
Man sieht, dass 
f
 
−
x
 nicht gleich 
f
 
x
 ist. Also ist der Graph nicht achsensymmetrisch zur y-Achse.

  • Punktsymmetrie zum Ursprung?
Kriterium:
f
 
−
x
=
−
f
 
x
f
 
−
x
=
5x
2
−
x
3
−
2x
=
5x
2
−
1
·
x
3
+
2x
=
−
1
·
5x
2
x
3
+
2x
=
−
1
·
f
 
x
=
−
f
 
x
Also gilt:
f
 
−
x
=
−
f
 
x
Der Graph der Funktion ist punktsymmetrisch zum Ursprung.
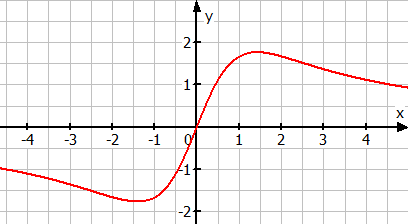
graphik
Zu c)
  • Achsensymmetrie zur y-Achse?
Kriterium:
f
 
x
=
f
 
−
x
f
 
x
=
5x
2
x
3
+
2
f
 
−
x
=
5
·
−
x
2
−
x
3
+
2
=
5x
2
−
x
3
+
2
Man sieht, dass 
f
 
−
x
 nicht gleich 
f
 
x
 ist. Also ist der Graph nicht achsensymmetrisch zur y-Achse.

  • Punktsymmetrie zum Ursprung?
Kriterium:
f
 
−
x
=
−
f
 
x
f
 
−
x
=
5x
2
−
x
3
+
2
−
f
 
x
=
−
5x
2
x
3
+
2
Man sieht, dass 
f
 
−
x
 nicht gleich 
−
f
 
x
 ist. Also ist der Graph nicht punktsymmetrisch zum Ursprung.
Der Graph der Funktion ist also weder achsensymmetrisch zur y-Achse noch punktsymmetrisch zum Ursprung.
graphik
Beispiel 2
Untersuche, ob der Graph der Funktion achsensymmetrisch zur y-Achse oder punktsymmetrisch zum Ursprung ist.
a) 
f
 
x
=
x
−
2
·
x
+
2
b) 
f
 
x
=
−
0,4x
3
+
2x
c) 
f
 
x
=
0,1x
−
0,3
·
0,5
−
2x
Zu a)
Um Aussagen über die Symmetrie des Graphen treffen zu können, muss man den Funktionsterm ausmultiplizieren:
f
 
x
=
x
−
2
·
x
+
2
=
x
2
−
4
    (3. binomische Formel)
Der Funktionsterm enthält nur x-Potenzen mit geraden Hochzahlen:
f
 
x
=
x
2
−
4
·
x
0
Also ist der Graph achsensymmetrisch zur y-Achse.
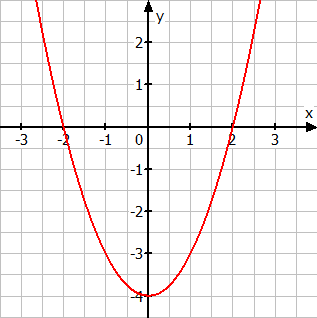
graphik
Zu b)
Der Funktionsterm enthält nur x-Potenzen mit ungeraden Hochzahlen:
f
 
x
=
−
0,4x
3
+
2x
1
Also ist der Graph punktsymmetrisch zum Ursprung.
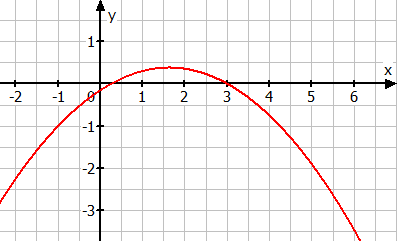
graphik
Zu c)
Um Aussagen über die Symmetrie des Graphen treffen zu können, muss man den Funktionsterm ausmultiplizieren:
f
 
x
=
0,1x
−
0,3
·
0,5
−
2x
=
0,05x
−
0,2x
2
−
0,15
+
0,6x
=
−
0,2x
2
+
0,65x
−
0,15
   
Der Funktionsterm enthält x-Potenzen mit geraden und ungeraden Hochzahlen:
f
 
x
=
−
0,2x
2
+
0,65x
1
−
0,15
·
x
0
Also ist der Graph weder achsensymmetrisch zur y-Achse noch punktsymmetrisch zum Ursprung.
(Hinweis: Das heißt aber nicht, dass er gar keine Symmetrie aufweist. Am Schaubild erkennt man, dass der Graph achsensymmetrisch ist und die Symmetrieachse durch den Scheitel verlaufen muss.)
graphik
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen