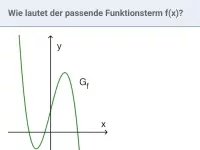
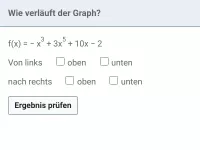
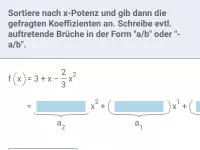
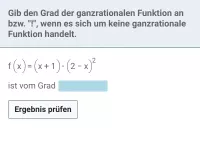
Was ist eine ganzrationale Funktion und welche Begriffe sind damit verbunden?
Der Term f(x) einer ganzrationalen Funktion (synonym: Polynomfunktion) besteht aus einer Summe von x-Potenzen, denen reelle Faktoren vorangestellt sind, wie z.B.
½ x³ + 3x² − 5
Die höchste x-Potenz bestimmt den Grad, im Beispiel oben beträgt dieser 3. Die vor den x-Potenzen stehenden reellen Faktoren (½; 3; -5) nennt man Koeffizienten. Taucht eine x-Potenz gar nicht auf, so ist der entsprechende Koeffizient 0.
Beispiel
f(x) | = |
|
Gib den Grad und die auftretenden Koeffizienten ai an (mit ai ist der Faktor vor xi gemeint)
Lösung:
- Da x4 die höchste x-Potenz ist, handelt es sich um ein Polynom vom Grad 4.
- Vor x2 steht ein "−", also ist a2 = -1.
- Vor x4 steht der Faktor 2, also ist a4 = 2
- x3 und x1 (also x) kommen nicht vor, daher a3 = a1 = 0
- Dann gibt es noch den konstanten Summanden "4/7" (sozusagen der Koeffizient vor x0), daher a0 = 4/7.
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Wie bestimmt man das Verhalten des Graphen einer ganzrationalen Funktion an den Rändern?
- Was bedeutet die faktorisierte Form ganzrationaler Funktionen und wie wird sie in Summenform umgewandelt?
- Wie bestimmt man den Grad einer ganzrationalen Funktion in Summen- und Produktform?
- Wie erkennt man Achsen- und Punktsymmetrie bei Funktionen, insbesondere bei ganzrationalen Funktionen?