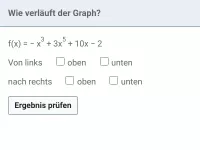
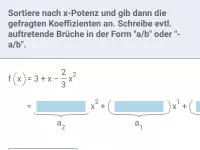
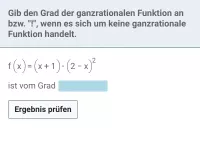
Wie bestimmt man den Grad einer ganzrationalen Funktion in Summen- und Produktform?
Um den Grad anzugeben, schaut man auf die höchste x-Potenz (sofern der Term als Summe von x-Potenzen mit jeweiligem Koeffizient vorliegt).
Liegt der Term faktorisiert vor, muss man pro Faktor die größte x-Potenz heranziehen. Es ist (für die Bestimmung des Grads) nicht erforderlich, alle Klammern auszumultiplizieren.
Beispiel
Bestimme den Grad von
a)
| = |
|
b)
| = |
|
Lösung:
a)
ist die x-Potenz mit dem höchsten Exponent, also
.
x | 5 |
|
b) Quadriert man die erste Klammer, so ergibt sich
als höchste x-Potenz. In der zweiten Klammer ist
die höchste x-Potenz. Multipliziert man beide Klammern, so ergibt sich
als insgesamt höchste x-Potenz. Also gilt auch hier
.
x | 2 |
x | 3 |
| = |
|
|
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Was ist eine ganzrationale Funktion und welche Begriffe sind damit verbunden?
- Wie bestimmt man das Verhalten des Graphen einer ganzrationalen Funktion an den Rändern?
- Was bedeutet die faktorisierte Form ganzrationaler Funktionen und wie wird sie in Summenform umgewandelt?
- Wie erkennt man Achsen- und Punktsymmetrie bei Funktionen, insbesondere bei ganzrationalen Funktionen?