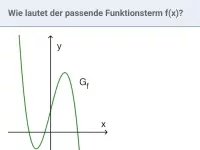
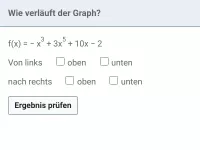
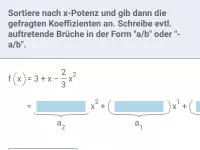
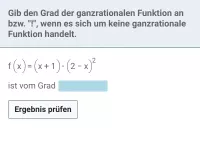
Was bedeutet die faktorisierte Form ganzrationaler Funktionen und wie wird sie in Summenform umgewandelt?

Ein ganzrationaler Term kann evtl. in faktorisierter Form vorliegen, d.h. als Produkt von mehreren Teiltermen (jeder davon ebenfalls ganzrational). Um die übliche Darstellung zu erhalten (Summe von x-Potenzen mit jeweiligem Koeffizient), muss man die Klammern ausmultiplizieren. Dabei ist das Distributivgesetz ("jeder mit jedem") anzuwenden.
Beispiel
f
 
x
=
1
2
 
x
−
3
·
x
+
1
3
2
. Multipliziere aus und gibt die Koeffizienten 
a
0
, a
1
, a
2
 usw. an, die vor 
x
0
, x
1
, x
2
 usw. stehen.
Lösung:
1
2
 
x
−
3
·
x
+
1
3
2
=
1
2
 
x
−
3
·
x
2
+
2
3
 
x
+
1
9
binomische Formel
=
1
2
 
x
3
+
1
3
 
x
2
+
1
18
 
x
−
3x
2
−
2x
−
1
3
jeder mit jedem
=
1
2
 
x
3
−
2
 
2
3
 
x
2
−
1
 
17
18
 
x
−
1
3
zusammengefasst
a
0
=
−
1
3
, 
a
1
=
−
1
 
17
18
, 
a
2
=
−
2
 
2
3
, 
a
3
=
1
2
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen