Wie bestimmt man das Verhalten des Graphen einer ganzrationalen Funktion an den Rändern?
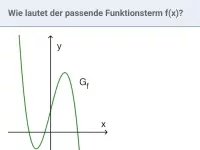
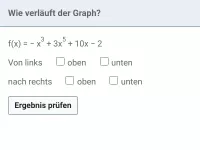
Bei einer ganzrationalen Funktion entscheidet die größte x-Potenz mitsamt ihrem Koeffizienten, von wo der Graph kommt und wohin er geht:
- Exponent ungerade, Koeffizient positiv (z.B. 5x³): von links unten nach rechts oben
- Exponent ungerade, Koeffizient negativ (z.B. -2x): von links oben nach rechts unten
- Exponent gerade, Koeffizient positiv (z.B. ½x²): von links oben nach rechts oben
- Exponent gerade, Koeffizient negativ (z.B. -x²): von links unten nach rechts unten
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Was ist eine ganzrationale Funktion und welche Begriffe sind damit verbunden?
- Was bedeutet die faktorisierte Form ganzrationaler Funktionen und wie wird sie in Summenform umgewandelt?
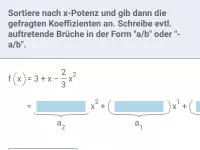
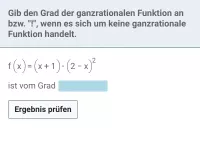
- Wie bestimmt man den Grad einer ganzrationalen Funktion in Summen- und Produktform?
- Wie erkennt man Achsen- und Punktsymmetrie bei Funktionen, insbesondere bei ganzrationalen Funktionen?