Was versteht man unter einer behebbaren Definitionslücke?

Eine Definitionslücke ist (anders als bei einer Polstelle) behebbar, wenn der "problematische" Faktor im Nenner herausgekürzt werden kann. Zur näheren Bestimmung von Nullstellen, Polstellen und (evtl. behebbaren) Definitionslücken sollte man also wie folgt vorgehen:
  1. Zähler und Nenner so weit wie möglich faktorisieren
  2. Definitionsmenge bestimmen: ALLE auftretenden Faktoren im Nenner, die Null werden können, liefern eine Definitionslücke (ganz gleich, ob man sie herauskürzen kann oder nicht)
  3. Definitionslücken näher spezifizieren: behebbar, wenn herauskürzbar; ansonsten Polstelle
  4. Nullstellen bestimmen: nur solche Faktoren im Zähler, die nicht herausgekürzt werden können, liefern Nullstellen der Funktion.
Beispiel
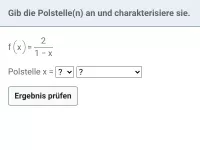
Bestimme evtl. auftretende Nullstellen und Definitionslücken und charakterisiere diese näher.
f(x)
=
4
−
6x
9x
3
−
4x
  • Definitionslücken
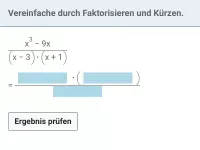
Faktorisierung des Nenners, um die Definitionslücken ablesen zu können:
9x
3
−
4x
=
x
 
9x
2
−
4
=
x
·
3x
−
2
·
3x
+
2
Erläuterung: im ersten Schritt wird x ausgeklammert, im zweiten die 3. binom. Formel angewandt.
Daraus ergeben sich drei Definitionslücken 
x
1
=
0
 und 
x
2,3
=
±
2
3
.

  • Nullstellen
Der Zähler wird nur null für 
x
=
2
3
. Da diese Stelle nicht definiert ist (siehe oben) liegt für f somit keine Nullstelle vor.

  • Charakterisierung der Definitionslücken
Zunächst sollte man den Bruchterm kürzen, um sich bei den nachfolgenden Betrachtungen leichter zu tun. Dass man kürzen kann ergibt sich aus der Tatsache, dass sowohl der Zähler als auch der Nenner für 
x
=
2
3
 den Wert null annimmt.
f
 
x
=
2
·
2
−
3x
x
·
3x
−
2
·
3x
+
2
=
−
2
·
−
2
+
3x
x
·
3x
−
2
·
3x
+
2
=
−
2
x
·
3x
+
2
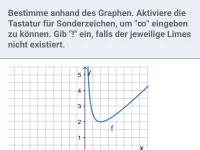
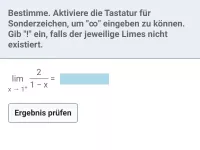
Untersuche jetzt das Verhalten an den einzelnen Definitionslücken:
x
1
=
0
lim
x→0−
 
−
2
x
·
3x
+
2
=
"
 
−
2
0−
·
2
 
"
=
"
 
−
2
0−
 
"
=
∞
Da es sich um eine einfache Polstelle handelt, also mit Vorzeichenwechsel (VZW), kann man auf die Grenzwertbetrachtung von rechts verzichten und bereits jetzt festhalten, dass es sich um eine Polstelle mit VZW +/− handelt.
x
2
=
2
3
lim
x→
2
3
    
−
2
x
·
3x
+
2
=
−
2
2
3
·
4
=
−
0,75
An dieser Stelle liegt also eine behebbare Definitionslücke vor, der Graph hat ein Loch im Punkt 
2
3
 
|
 
−
0,75
.
x
3
=
−
2
3
lim
x→
−
2
3
−
    
−
2
x
·
3x
+
2
=
"
 
−
2
−
2
3
·
0−
 
"
=
"
 
−
2
0+
 
"
=
−
∞
Einfache Polstelle, daher Polstelle mit VZW −/+
Gebrochen-rationale Funktion, Nullstellen, Polstellen, behebbare Definitionslücken, Bsp
Lernvideo

Gebrochen-rationale Funktion, Nullstellen, Polstellen, behebbare Definitionslücken, Bsp

Kanal: Mathegym
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen